05. Recursivitat I

Última modificació per editor1 el 2021/04/23 16:46

Continguts

Objectius
Introducció
Definició
Principi d'inducció
- Exemple 05_01
- Exemple 05_02
Principis dels algorismes recursius
Resum

Objectius

Els objectius d'aquest mòdul són el següents:

Revisar el concepte de recursivitat vist a Fonaments de Programació.
Entendre els principis bàsics de les definicions i mètodes recursius, i ser capaç d'escriure mètodes recursius senzills.
Entendre la diferència entre recursivitat i iteració, i els avantatges de cadascun d'ells.
Comprendre la diferència entre recursivitat directa i indirecta.

Introducció

A Fonaments de Programació es va introduir el concepte de recursivitat. En aquest mòdul revisarem la definició i veurem uns quants exemples més d’algorismes recursius.

També es farà una comparativa dels avantatges i desavantatges dels algorismes recursius, i s’analitzarà com passar un algorisme recursiu a un algorisme iteratiu.

Definició

Recordem primer que el concepte de recursivitat no es redueix a algorismes. De fet, és diu que un objecte és recursiu quan es defineix en funció de si mateix. El podem trobar en molts camps com la natura, l’art, i en les matemàtiques, entre d’altres.

Per exemple, en moltes de les formes trobades a la natura podem observar que les formes més grans contenen copies més petites de si mateixa, i al mateix temps, les petites també contenen còpies de si mateixa.

També podem veure el concepte de recursivitat en les nines russes o en quadres, on el tema pintat es conté a si mateix. I de fet utilitzem recursivitat en la vida quotidiana quan, per exemple fem una fotocopia d’un fotocopia o fotografiem una fotografia.

Per exemple, les següents imatges mostren algun exemples de recursivitat:

També, com es veu a Fonaments de Programació al mòdul de recursivitat a les matèmatiques s'utiliza per la definció de conceptes, com per exemple:

Els nombres naturals.
Els parells.
El factorial d'un nombre natural.

Un altre exemple de matemàtiques és triangles de Sierpinski, en el que cada triangle està format per d’altres més petits, que al mateix temps estan formats d’altres més petits de manera recursiva.

triangle de Sierpinski.png

Com podem veure, doncs, la recursivitat està present al nostre voltant. El que volem fer ara és analitzar com es pot aplicar el concepte als algorismes informàtics. En quin cas podem utilitzar un mètode recursiu? Com el dissenyem i comprovem que funciona correctament? Aquestes són algunes preguntes que ens de fem, i com veurem en aquest mòdul i el següent, la dificultat de la recursivitat no està en la programació en si mateixa sinó en el disseny dels algorismes recursius.

Principi d'inducció

Per resoldre problemes recursius cal raonar de manera similar a com es fa quan s’utilitza el Principi d’inducció en demostracions matemàtiques sobre els nombre naturals.

Recordem com funciona el principi d’inducció. Per demostrar una propietat del nombres naturals cal fer els següents dos passos:

Demostrar que és vàlida pel cas més simple, normalment pel cas n= 0 (en algun cas el cas més simple pot ser 1 o 2)

Demostrar que si és cert per n-1 també ho és per n.

Veiem un parell d’exemples:

Exemple 05_01

Demostrar que la suma dels n primers nombres naturals és igual a 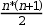$\frac{n*(n+1)}{2}$ , és a dir:

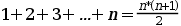
$1+2+3+ ...+ n = \frac{n*(n+1)}{2}$

Base d’inducció: cal provar que la fórmula és certa pel cas n = 1. Si substituïm a la fórmula n per 1 tenim:

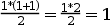
$\frac{1*(1+1)}{2} = \frac{1*2}{2} = 1$

Per tant podem dir que el cas base és cert.

Hipòtesis d’inducció: suposem que la fórmula és certa per n. És a dir ...

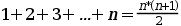
$1+2+3+ ...+ n = \frac{n*(n+1)}{2}$

... és cert.

Demostració: ara hem de demostrar també ho és per n+1.

Com ho plantegem? Sabem que ...

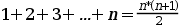
$1+2+3+ ... + n = \frac{n*(n+1)}{2}$

... és cert i hem de demostrar que ho és per n+1.

Si escrivim la fórmula per n+1 tenim el següent, que cal demostrar:

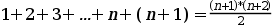
$1+2+3+ ... + n + (n+1) = \frac{(n+1)*(n+2)}{2}$

Com hem suposat que per n la fórmula és certa, podem substituir:

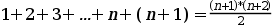
$1+2+3+ ... + n + (n+1) = \frac{(n+1)*(n+2)}{2}$

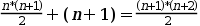
$\frac{n*(n+1)}{2} + (n+1) = \frac{(n+1)*(n+2)}{2}$

I fent operacions tenim:

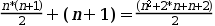
$\frac{n*(n+1)}{2} + (n+1) = \frac{(n^2+2*n+n+2)}{2}$

Si fem operacions a la part esquerra ens queda:

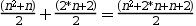
$\frac{(n^2+n)}{2}+\frac {(2*n+2)}{2} = \frac{(n^2+2*n+n+2)}{2}$

I podem veure que les dues expressions són realment iguals.

Comentaris

La inducció funciona de tal manera que tenim un cas base que podem demostrar que és cert. I demostrem també que si és cert per n ho és per n+1.

Per tant podem dir que:

És cert per n = 1 (demostrat).
Com és cert que per n = 1, aplicant la inducció sabem que és cert per n = 2.
Com és cert que per n= 2, aplicant la inducció sabem que és cert per n = 3.
Etc, ect. És a dir, podem dir que és cert per qualsevol valor de n.

Exemple 05_02

Suposem que volem demostrar que:

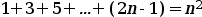
1 _ 3 _ 5 _ ... _ (2n - 1) = n^2

Per demostrar-ho per inducció fem el següent:

Base d’inducció

Hem de demostrar-ho per n=1. Si substituïm tenim que ...

1 = 1^2

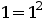
... és cert.

Hipòtesis d’inducció

Suposem que és cert per n, és a dir que ...

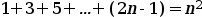
1 _ 3 _ 5 _ ... _ (2n - 1) = n^2

... és cert.

Demostració

Ara hem de demostrar que és cert per n+1. Per fer-ho escrivim la fórmula per n+1. Seria:

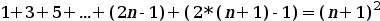
1 + 3 + 5 + ... + (2n - 1) + (2*(n +1) -1) = (n+1)^2

Utilitzem la hipótesi d'inducció i substituïm:

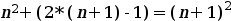
n^2 + (2*(n +1) - 1) = (n+1)^2

Si operem a les dues bandes tenim:

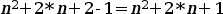
n^2 + 2*n + 2 - 1 = n^2 + 2*n + 1

Que resulta:

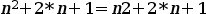
n^2 + 2*n + 1 = n2 + 2*n + 1

O sigui que efectivament la fórmula és certa.

Principis dels algorismes recursius

La recursivitat es basa en la inducció. A l’igual que en la inducció, per la recursivitat necessitem un cas base que fa que la recursivitat es pari. El cas base ha de ser un cas pel que sabem segur quin és el resultat. I el cas recursiu, on es defineix el terme n-èssim en funció del terme anterior o anterior.

Per exemple:

Pel factorial sabem que 1! = 1, per la resta n! = n*n(-1)
Per Fibonacci sabem que fib(1)=1 i fib(2)=1 per la resta fib( n )= fib(n-1) + fib(n-2)
Per una multiplicació a*b, si b=1 sabem que a*1 = a per la resta és a*(b-1)*b

A continuació anem a veure uns quants exemples d'algorismes recursius:

Exemple 05_03: palíndroms

Anem a veure com escriure un algorisme recursiu per decidir si una cadena de caràcters és un palíndrom. Recordem que un text és diu que és un palíndrom si es llegeix igual de esquerra a dreta que de dreta a esquerra. Alguns exemples de palíndroms:

Madam, I’m Adam
A global rotator lab, Olga
Revenge Meg, never!
A Tirana mana Rita
Lúcid, irònic, i no ridicul.

Per decidir si la cadena és un palíndrom cal treure tots els espais en blanc, símbols de puntuació i no tenir en compte els accents.

Si pensem en com resoldre el problema és fàcil veure que té una solució que es pot formular de manera recursiva. Per decidir si una cadena és un palíndrom fem el següent:

Si la cadena té un únic caràcter o és buida la cadena és un palíndrom.
Si la primera i la última lletra són diferents ja sabem que no es tracta d’un palíndrom. Si són iguals, la cadena serà un palíndrom si la sub cadena que queda de treure la primera i última lletra és un palíndrom.

Per tant la definició de la solució és recursiva.

Cas base: mirar la longitud de la cadena. Si és 0 o 1 retornar cert.

Recursió: mirar si els extrems són iguals. Si ho són retornem el valor resultant d’analitzar la subcadena resultant de treure els extrem.

Anem a veure com escrivim l’algorisme.

Definim primer els tipus de dades. En aquest hem de tenir una taula de caràcters per guardar la cadena. Podríem definir-la de la següent manera:

Algorisme
C

const
MAX_LETTERS: integer = 200;
end const

type
    tSentence = record
        sentence: array [MAX_LETTERS] of char;
        numChars: integer;
    end record
end type

/* program presentació */
#define MAX_LETTERS 200

typedef enum {FALSE, TRUE} boolean;

typedef struct {
char *sentence;
int numChars;
} tSentence;

Mirem ara quina ha de ser la capçalera de la funció. Hi ha diferents maneres d’implementar-lo. En aquest optarem per passar sempre la cadena completa i dos enters que indicaran l’inici i final de la subcadena que cal analitzar.

Amb aquest supòsit, la capçalera del mètode seria:

Algorisme
C

function isPalindrome(sentence: tSentence, posIni: integer, posFinal: integer): boolean;

typedef enum {FALSE, TRUE} boolean;

boolean isPalindrome(tSentence sentence, int posIni, int posFinal);

Cas Base: les condicions que faran parar la recursivitat seran quan la cadena analitzada tingui longitud 0 o 1. Si la cadena té un únic caràcter podem dir que es tracta d’un palíndrom. Per defecte també considerem palíndrom el cas en que la cadena sigui buida.

Cas recursiu: retornarà el resultat de comparar els extrems i el resultat de cridar recursivament a si mateixa traient els extrems.

La funció quedaria:

Algorisme
C

function isPalindrome (sentence: tSentence, posIni: integer, posFinal: integer): boolean

    if posIni ≥ posFInal then
        return true;
    else
        return (sentence.sentence[posIni] = sentence.sentence[posFInal]) and isPalindrome(sentence, posIni+1, posFinal-1)
    end if
end function

typedef enum {FALSE, TRUE} boolean;

boolean isPalindrome(tSentence sentence, int posIni, int posFinal) {

   if (posIni >= posFinal) {
       return TRUE;
    } else {
       return (sentence.sentence[posIni] == sentence.sentence[posFinal]) && isPalindrome(sentence, posIni+1, posFinal-1);
    }
}

Ara falta definir el programa principal que farà la primera crida a isPalindrome. Per simplificar l’exemple, suposarem que la cadena entrada ja no té ni espais ni signes de puntuació. En el cas que no fos segur, caldria cridar primer a un mètode que neteges la cadena inicial traient blanc, signes de puntuació i accents.

Algorisme
C

const
MAX_LETTERS: integer = 200;
end const

type
    tSentence = record
        sentence: array [MAX_LETTERS] of char;
        numChars: integer;
    end record
end type

algorithm palindrome

    var
        sentence: tSentence;
    end var

    writeString("Enter and alphabetical string with no blanks");
    sentence.sentence = readString();
    sentence.numChars = length(sentence.sentence);

    if isPalindrome(sentence, 1, sentence.numChars) then
        writeString("It is a palndrome");
    else
        writeString("It is not a palindrome");
    end if

end algorithm

function isPalindrome(sentence: tSentence, posIni: integer, posFinal: integer): boolean

end function

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <string.h>

#define MAX_LETTERS 200

typedef enum {FALSE, TRUE} boolean;

typedef struct {
   char *sentence;
   int numChars;
} tSentence;

boolean isPalindrome(tSentence sentence, int posIni, int posFinal);

int main(void) {

    tSentence sentence;
    sentence.sentence = malloc(MAX_LETTERS*sizeof(char));
    printf("Enter and alphabetical string with no blanks\n");
    scanf("%[^\n]", sentence.sentence);
    fflush(stdin);
    sentence.numChars = strlen(sentence.sentence);

   if (isPalindrome(sentence, 0, sentence.numChars-1)) {
        printf("It is a palindrome");
    } else {
        printf("It is not a palindrome");
    }

   return 0;
}

boolean isPalindrome(tSentence sentence, int posIni, int posFinal) {

   if (posIni >= posFinal) {
       return TRUE;
    } else {
       return (sentence.sentence[posIni] == sentence.sentence[posFinal] && isPalindrome(sentence, posIni+1, posFinal-1);
    }
}

El dibuix següent mostra la seqüència de crides que farà el programa si utilitzem la cadena "revengemegnever"

05+01.svg

Exemple 05_04: potència de dos nombres

Una manera de calcular la potencia de dos enters és calculant-lo de la següent manera:

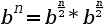$b^n = b^\frac{n}{2} * b^\frac{n}{2}$ si n es parell.
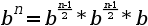$b^n = b^\frac{n-1}{2} * b^\frac{n-1}{2} * b$ si n és senar

Aplicant aquesta definició podem escriure un funció recursiva que calculi la potencia de dos enters.

Algorisme
C

function power (base: integer, exp: integer): integer

    var
        temp: integer;
    end var

    if exp = 1 then
        return base;
    else
        if exp mod 2 = 0 then
            temp = power(base, exp div 2);
            return temp*temp;
        else
             temp = power(base, (exp-1) div 2);
             return temp*temp*base;
        end if
    end if

end function

algorithm computePower

    var
        base: integer;
        exp: integer;
    end var

    base := readInteger();
    exp := readInteger();
    writeInteger(power(base, exp));

end algorithm

#include <stdio.h>

int power(int base, int exp);

int main(void) {

   int base;
   int exp;

    scanf("%d", &base);
    scanf("%d", &exp);

    printf("%d\n", power(base, exp));

   return 0;
}

int power(int base, int exp) {

   int temp;

   if (exp == 1) {
       return base;
    } else if (exp%2 == 0) {
        temp = power(base, exp/2);
       return temp*temp;
    } else {
        temp = power((base), (exp-1)/2);
       return temp*temp*base;
    }
}

La seqüència de crides que es faran si calculem 2 a la 10 serà la següent:

power(2,10)
     power(2,5)
        power(2,2)
            power(2,1)
            return 2
         return 2 * 2
      return 4 * 4 * 2
return 32 * 32

Exemple 05_05: sèrie de Fibonacci

En aquest exemple veurem un cas en que la solució recursiva, encara que és elegant no és gent eficient.

Calcular un element de la sèrie de Fibonacci recursivament és fàcil i elegant, ja que la pròpia definició de la sèrie ho és. Recordem la definició:

Si n = 1 llavors f(1) = 1
Si n = 2 llavors f(2) = 1
Per qualsevol altre valor de n f( n ) = f(n-1) + f(n-2)

En aquest cas, la definició ja ens dona el cas base pels valors de n igual a 1 i 2, i també la pròpia definició dona la recursivitat.

La implementació recursiva quedaria de la següent manera:

Algorisme
C

algorithm fibonacci

    var
        n: integer;
        result: integer;
    end var

    writeString("Enter a positive integer number");
    n := readInteger();
    result := fib( n );
    writeString("the n-th element of the Fibonacci series is:");
    writeInteger(result);

end algorithm

function fib(n: integer)

    if n=1 or n=2 then
        return 1
    else
        return (fib(n-1) + fib(n-2))
    end if

end function

#include <stdio.h>
#include <conio.h>

int fib(int n);

int main(void) {

   int n;
   int result;

    printf("Enter a positive integer number");
    scanf("%d", &n);
    result = fib( n );
    printf("The n-th element of the Fibonacci series is: %d\n", result);

   return 0;
}

int fib(int n){

   if (n==1 || n==2) {
       return 1;
    } else {
       return (fib(n-1)+fib(n-2));
    }
}

L’algorisme és fàcil d’entendre però és molt poc eficient. Per exemple, per calcular fib( n ) cal calcular fib(n-1) y fib(n-2), però per calcular fib(n-1) es torna a calcular fib(n-2).

En el dibuix es poden veure les crides que es faran amb la recursivitat en el cas de n=5. Per cada pas es fan dos crides menys quan arriba a n=1 o n=2 que retorna directament 1. Com podem veure, es fan crides repetides fent que l’algorisme no sigui eficient.

En aquest cas és millor utilitzar un algorisme iteratiu on es calcula el nombre de Fibonacci de manera incremental.

Exemple 05_06: com invertir les xifres d'un nombre natural

Suposem que ens demanen que invertim les xifres d'un nombre natural. El primer que podem pensar és una solució iterativa, però també hi ha una solució recursiva, que no és evident.

Veiem primer la següent taula que ens donarà una pista de com fer l'algorisme.

És a dir, si tenim el nombre 1234567, per exemple, el que cal fer és:

Pas	Nombre original	Nombre mod 10	Construcció del nombre invers	Comentari
1	1234567	7	0*10 + 7 = 7	Agafem el nombre que estem contruint(de moment 0) el multipliquem per 0 i si sumen l'última xifra
2	123456	6	7*10 + 6 = 76	Repetim l’operació anterior
3	12345	5	76*10 + 5 =765	Repetim l’operació anterior
4	1234	4	765*10 + 4 = 7654	Repetim l’operació anterior
5	123	3	7654*10 + 3 = 76543	Repetim l’operació anterior
6	12	2	76543*10 + 2 = 765432	Repetim l’operació anterior
7	1	1	765432*10 + 1 = 7654321	Repetim l’operació anterior
8	0	0		S’acaba el procés

Pel que veiem, l’invers l'anem construint a mida que es van fer les crides recursives. Això és necessari perque la xifra menys significativa caldrà multiplicar-la per 10 a la n, però a priori no sabem el valor de n. Si a cada crida multipliquem per 10, al final la xifra menys significativa ocuparà el lloc que li toca en el nombre invers.

Per tant definirem una funció a la que li passarem dos paràmetres, el nombre que volem invertir i el que anem construint. Quan arribem al final retornarem el construït.

És a dir, la capçalera serà:

Algorisme
C

function reverse(number: integer, temp: integer): integer

int reverse(unsigned int number, unsigned int temp);

Cas base: serà quan number sigui 0 (ja no queden xifres). Quan ja no en queden la funció retorna el segon paràmetre, que és el nombre que anem construint.

Cas recursiu: cridem la funció recursiva passant com primer paràmetre number div 10 i com segon el que anem construint.

Algorisme
C

function reverse(number: integer, temp: integer): integer

    if number = 0 then
        return temp;
    else
        return reverse(number div 10, temp*10 + number mod 10);
    end if

end function

algorithm reverseRec

    var
        num, result: integer;
    end var

num := readInteger();
writeInteger(reverse(num, 0));

end algorithm

#include <stdio.h>

unsigned int reverse(unsigned int number, unsigned int temp) {

   if (number == 0) {
       return temp;
    } else {
       return reverse(number/10, temp*10 + number%10);
    }
}

int main(void) {

   unsigned int num;
   unsigned int result;

    printf("Write a natural numbrer: ");
    scanf("%d", &num);
    result = reverse(num, 0);
    printf("%d\n", result);

   return 0;
}

Resum

En aquesta unitat hem revisat el concepte de recursivitat i l'hem comparat al principi d'inducció matemàtica.

Hem vist que tot algorisme recursiu ha de tenir un cas base, que para la recursivitat i el cas recursiu que resolt el problema cridant-se a si mateix.

En la següent unitat, continuarem amb la recursivitat. Analitzarem els diferents tipus de recursivitat, veurem com passar de recursiu a iteratiu i veurem uns quants exemples més d'algorismes recursius.

Etiquetes:

[_]

Creat per editor1 el 2018/09/16 23:06