Recursivitat
Objectius
- Presentar el concepte de recursivitat.
- Conèixer alguns exemples de procediments recursius.
- Entendre el pas del sistema iteratiu al recursiu.
Introducció
El concepte de recursivitat fa referència al fet que un algorisme s’utilitzi a si mateix per a resoldre un problema. El concepte en si és molt senzill i alhora molt potent, ja que molts problemes es poden plantejar de forma recursiva. Si un problema es pot arreglar amb solucions o versions més petites del mateix problema i aquestes versions més petites el poden reduir a casos trivials, podem utilitzar un algorisme recursiu per a resoldre’l. Aquesta unitat només vol donar una noció bàsica del concepte de recursivitat, per la qual cosa les explicacions es faran sobre exemples.
1. Exemple 1: nombres naturals
Els nombres naturals tenen la seva definició recursiva en matemàtiques:
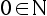
- Si
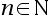llavors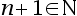 
El conjunt de nombres naturals és el mínim conjunt que compleix aquestes dues propietats.
Veiem que en aquest cas, per a definir què és un nombre natural, ho fem recursivament, o sigui, a partir de saber que n és recursiu, sabem que n _ 1 també ho és o, dit d’una altra manera, si volem saber si n és un nombre natural, hem de veure si aquest és 0, o si n-1 és natural. Llavors, si volem saber si un nombre és natural o no, ho podríem fer amb el següent algorisme:
function isNatural(n: integer) : boolean
if n=0 then
return true;
end if
return isNatural(n-1);
end function
tBoolean isNatural(int n) {
if(n==0) {
return TRUE;
}
return isNatural(n-1);
}
En aquest codi veiem un exemple dels dos elements que tot algorisme recursiu ha de tenir:
- Condició de finalització (en aquest cas quan n és 0).
- Regla recursiva (una crida recursiva amb n-1).
Per a entendre el que està passant cal tenir en compte que, malgrat ser la mateixa funció, cada crida a la funció isNatural s’afegeix a l’stack de memòria, amb la seva zona de memòria independent de la resta. A la figura següent se simula el que passaria a la memòria quan es crida isNatural(2) (s’ha obviat el mètode principal):
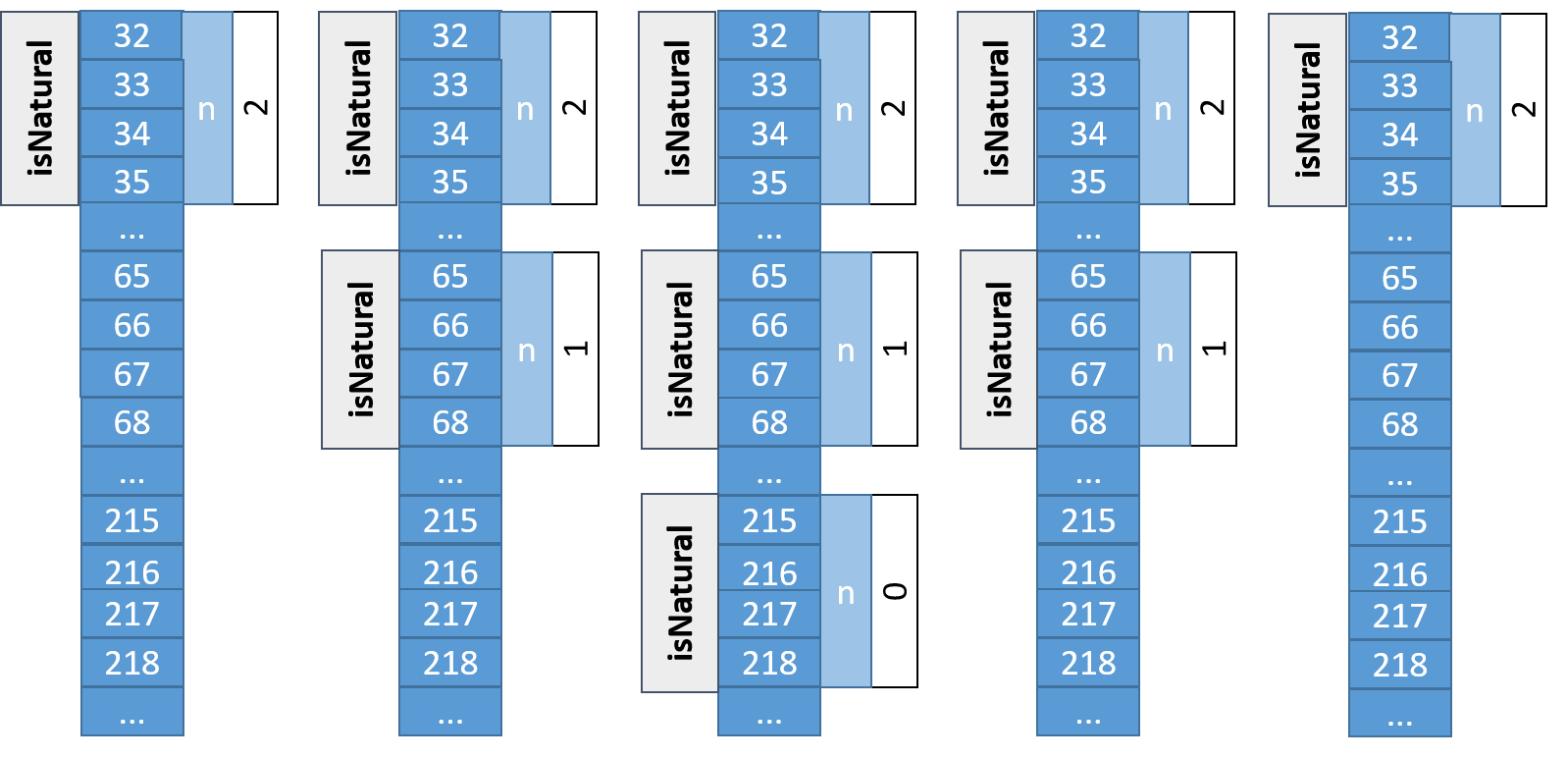
Veurem que quan es crida isNatural amb el valor 2, aquest queda guardat en una zona de memòria. Seguint amb l’algorisme, ja que n no és 0, es fa una altra crida a isNatural amb el valor 1. Aquesta nova crida s’afegeix a la pila i queda guardada en una altra zona de memòria diferent. Com que n encara no és 0, es torna a fer una crida a isNatural amb el valor 0 i aquesta nova crida també queda afegida a la pila utilitzant una altra zona de memòria. En aquest cas, com que el paràmetre té valor 0, es retornarà un true i es finalitzarà aquesta crida. Quan es finalitza l’execució d’una acció o funció, tota la memòria ocupada pels seus paràmetres i variables s’elimina i, per tant, ara solament quedaran les dues crides inicials a la memòria. La segona crida retornarà el valor true que ha retornat l’última crida i, per tant, finalitzarà i quedarà solament la primera crida a la memòria. Finalment aquesta crida inicial retornarà i també s’eliminarà de la memòria. L’important és veure que, encara que sigui la mateixa funció, a efectes pràctics és com si es tractés de funcions diferents i, per tant, els paràmetres i les variables que tingui són independents entre crides.
2. Exemple 2: factorial
El factorial d’un enter positiu n (escrit n!) es defineix com el producte de tots els nombres enters positius des d’1 fins a n. És a dir:
n! = 1 x 2 x 3 x ... x (n-1) x n
Una possible implementació de la funció factorial utilitzant estructures iteratives podria ser:
function fact(n: integer) : integer
var
i : integer
f : integer
end var
f:=1;
for i:=1 to n do
f:=f*i;
end for
return f
end function
unsigned int i=0;
unsigned int f=1;
for(i=1; i<=n ; i__) {
f*=i;
}
return f;
}
Si ho pensem de forma recursiva, podem veure que factorial(n) és el mateix que n x factorial(n-1). Per tant, podríem escriure-ho com:
function fact(n: integer) : integer
if n==1 then
return 1;
end if
return n*fact(n-1);
end function
if(n==1) {
return 1;
}
return n*fact(n-1);
}
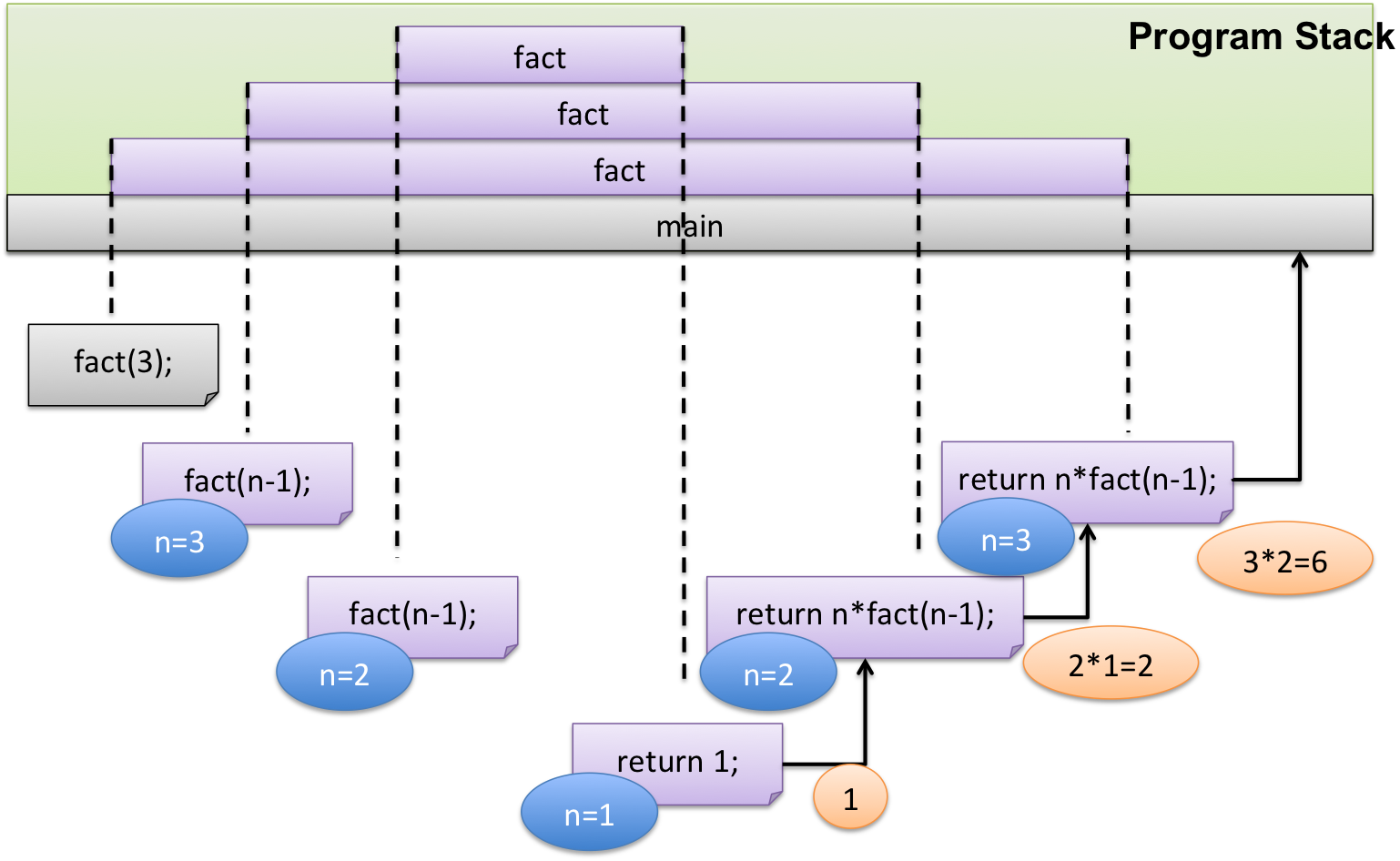
A continuació es mostra un esquema del que passaria a la pila de programes (program stack) si féssim una crida a aquest mètode per a n = 3 dins del programa principal main. D’esquerra a dreta es mostra l’evolució temporal, que correspon als passos següents:
- A la pila solament està el main.
- Quan des del main es crida fact(3), a la pila es fa un push de la informació referent a la funció fact. En aquest cas, el paràmetre n té un valor de 3, que és el que se li ha indicat a la crida.
- Com que n no té un valor igual a 1 es retorna el resultat de l’expressió n * fact(n-1)*. Com que el valor de n és 3, cal avaluar l’expressió 3 * fact(2), i per tant, es fa una crida a la funció fact passant com a paràmetre el 2.
- En fer la crida a fact(2), a la pila es fa un push de la informació referent a la funció fact, on, en aquest cas, el paràmetre n té un valor de 2.
- Com que n no té un valor igual a 1 es retorna el resultat de l’expressió n * fact(n-1). Com que el valor de n és 2, cal avaluar l’expressió 2 * fact(1), i per tant, cal fer una crida a la funció fact passant com a paràmetre l’1.
- Com que ara n té un valor igual a 1 , entra a l’if i retorna el valor 1. En el retorn es fa un pop de la pila, que elimina tota la informació de l’última funció que s’havia afegit.
- Atès que ara ja tenim el valor de fact(1), es pot avaluar l’expressió 2 * fact(1), i es retorna el valor 2. Quan fem el retorn, es fa un pop de la pila, eliminant tota la informació de l’última funció que s’havia afegit.
- Atès que ara ja tenim el valor de fact(2), es pot avaluar l’expressió 3 * fact(3) i es retorna el valor 6. En el retorn, es fa un pop de la pila, que elimina tota la informació de l’última funció que s’havia afegit, i solament deixa a la pila la informació de la funció main, que s’eliminarà quan aquesta finalitzi.
3. Exemple 3: tractament seqüencial
En general, la majoria dels algorismes que tracten seqüències són susceptibles de ser formulats de forma recursiva. Anem a veure un exemple simple: mostrar tots els elements d’un vector d’enters. Suposeu que tenim un vector de valors enters, finalitzat per un valor -1 que marca el final de la seqüència. Si el plantegéssim com un algorisme iteratiu, tindríem:
action writeVector(v: vector of integer)
var
i : integer
end var
i:=1
while v[i]<>-1 do
writeInteger(v[i]);
i:=i_1;
end while
end action
int i=0;
while(v[i]!=-1) {
printf("%d", v[i]);
i__;
}
}
Un plantejament recursiu seria mostrar el primer element de la seqüència i després tornar a cridar el mètode recursiu per a mostrar la resta dels elements. Anem processant cada element de la seqüència (en aquest cas simplement mostrar) fins a arribar a l’element que ens marca el final de la seqüència. Per a convertir-lo en recursiu, cal buscar la repetició d’un patró, per exemple, imaginem que tenim el vector següent:
{1, 2, 3, 4, -1}
La crida
writeVector({1, 2, 3, 4, -1})
és equivalent a mostrar el primer element i cridar:
writeVector({2, 3, 4, -1})
Per tant, veiem que podem dividir el problema en un altre més simple (és una part del problema inicial). A més, tenim un cas trivial, que és writeVector({-1}), en el qual no cal fer res, ja que tenim un vector sense cap element per mostrar. Per tant, podem definir una versió recursiva de la funció writeVector.
Vegem dues versions per a implementar aquest algorisme, una amb l’ús de funcions auxiliars i l’altra amb punters.
3.1. Funcions auxiliars
En alguns casos, el plantejament recursiu requereix introduir informació addicional per a poder controlar la recursivitat. Per a afegir aquesta informació caldrà crear una nova funció o acció amb paràmetres addicionals. En aquest cas, incorporarem l’índex de la primera posició de la seqüència que cal processar. Per a això, crearem una nova acció writeVector_aux que, a més del vector, tindrà la primera posició a processar. L’acció writeVector assignarà els valors inicials per al procés recursiu:
action writeVector_aux(v: vector of integer; i : integer)
if v[i]<>-1 then
writeInteger(v[i]);
writeVector_aux(v, i_1);
end if
end action
action writeVector(v: vector of integer)
writeVector_aux(v, 1);
end action
if(v[i]!=-1){
printf("%d", v[i]);
writeVector_aux(v, i_1);
}
}
void writeVector(int *v) {
writeVector_aux(v, 0);
}
3.2. Punters
Una altra possibilitat per a implementar aquest algorisme és l’ús de punters. En el cas concret de C, podem aprofitar el fet que un vector realment és un punter a la primera posició del vector i, per tant, no necessitem cap mètode auxiliar:
if(*v!=-1) {
printf("%d", *p);
writeVector(p_1);
}
}
En aquest cas, el que fem és mostrar el contingut del punter (que és el mateix que v[0]) i desplaçar el punter una posició abans de tornar a fer la crida recursiva.
Resum
En aquesta unitat hem conegut el concepte de programació recursiva en contrast amb la programació iterativa i hem vist alguns exemples senzills de la seva aplicació.