02. Especificació formal d'algorismes
Objectius
Els principals objectius d’aquest mòdul són els següents:
- Entendre què vol dir especificar un problema.
- Distingir entre especificació d’un problema (què s’ha de resoldre) i algorisme (com es resol el problema).
- Comprendre quins són els elements de l'especificació: variables d'entrada i sortida, precondició i postcondició.
- Aprendre els elements bàsics del llenguatge formal per especificar problemes (càlcul de predicats).
- Saber especificar problemes senzills.
Introducció
A Fonaments de Programació vàreu veure quins són els components dels llenguatges de programació (algorísmic i C) que ens permeten escriure algorismes que resolen problemes donats.
Ara be, el punt de partida per escriure un algorisme és precisament la descripció del problema que es vol resoldre. Aquesta tasca, que podria semblar senzilla, no sempre ho és ja que normalment s’utilitza el llenguatge natural per descriure el problema, i el llenguatge natural, per manca de formalitat, pot portar a ambigüitats i falta de claredat en la descripció dels problemes. Aquest ambigüitat por provocar el desenvolupament d’algorismes erronis i, per tant, una pèrdua de temps en la resolució final dels problemes.
Una manera de assegurar que l’enunciat és clar és utilitzar un llenguatge formal per escriure l’enunciat. Descriure un problema i el resultat esperat de manera formal s’anomena especificar el problema. Aquest mòdul tracta l’especificació i defineix els conceptes bàsics, introduint el llenguatge formal utilitzat per especificar. També inclou diversos exemples de com especificar problemes senzills.
Aproximació intuïtiva
Imaginem que uns pares contacten a una cangur per portar els fills a l’escola.
El problema a resoldre podria ser: recollir els nens a les 8:00 del matí i portar-los a l’escola.
Si l’encàrrec que fan a la futura cangur no es detalla més, la cangur es pot trobar amb sorpreses. Per exemple, estaran els nens vestits i preparats per marxar o caldrà vestir-los? A quina hora han d'arribar a l'escola? Aquests detalls són importants per poder complir amb èxit la tasca encomanada.
La cangur, per poder preparar el seu algorisme (solució del problema consistent amb les accions que haurà de fer per portar els nens a l’escola i temps que necessita) ha de saber com els trobarà i a quina hora han d'arribar a l'escola, entre d'altres. Cal formalitzar la situació de partida.
Per tant cal especificar el problema. Això vol dir indicar clarament el punt de partida i la situació final.
Una possible solució seria:
En el dibuix podem veure en el requadre de l’esquerra com s’especifica la situació inicial del problema. Diu que la situació de partida correcta per la cangur és que els nens estiguin a punt per marxar. D'altra banda, el requadre de la dreta indica quina ha de ser la situació final: els nens han de ser a la porta de l’escola abans de les 8:30 del matí.
Cal fixar-se que en cap moment es diu com han d'anar a l’escola. La manera de fer-ho es deixa al criteri de la cangur. És a dir, l’especificació no diu com resoldre el problema sino la situació inicial i la final. Cal remarcar que el que descriu l’especificació és el canvi d’estat de l’entorn. En aquest cas, l’entorn està format per els nens i on es troben. El canvi de l’entorn fa que els nens passin d’estar a casa a estar a l’escola.
En un entorn de programació, l’entorn és el conjunt de variables d'entrada i sortida del problema. Les variables que es pugui utilitzar durant la resolució no formen part de l'especificació sinó de la solució. L’especificació indicarà com ha de canviar l’entorn. És a dir, quina ha de ser la situació inicial i quina la final.
Elements de l’especificació
A l’apartat anterior hem vist de manera informal en que consisteix l’especificació d’un problema. Anem ara a formalitzar la definició de l’especificació.
L’especificació d’un algorisme consta de quatre parts:
- Elements que defineixen l’entorn: declaració de les variables d’entrada i sortida.
- Precondició: estat inicial de l’entorn.
- Nom de l’algorisme.
- Postcondició: estat final de l’entorn.
Variables: declaració de les variables necessàries per especificar el problema. Com ja hem dit seran aquelles sobre les que definirem condicions tant d’entrada com de sortida. Per cada variable indicarem el seu nom i el seu tipus. Els noms de les variables hauran de ser significatius.
Precondició: definició de la condició que s’ha de complir a l’inici de l’algorisme. Quins són els valor vàlids de les variables d’entrada.
Nom de l’algorisme: identificació de l'algorisme mitjançant el nom que li estem especificant. Hauria de ser el més significatiu possible.
Postcondició: definició de la condició que ha de complir l’estat final de l’algorisme. Valors finals de les variables.
Exemple 02_01
Suposem que ens demanen especificar un algorisme que donat un enter n positiu, calculi la suma dels n primers quadrats.
Variables: les dades d’entrada es redueixen en aquest cas a una única variable per representar l’enter, li direm number i en necessitem un altre per representar el resultat, l’anomenarem sum. Escrivim doncs:
var
number: integer;
sum: integer;
end var
int sum;
Precondició: a la precondició hem d’indicar l’estat inicial de l’entorn que ens permetrà que l’algorisme s'executi correctament i retorni el valor esperat. En aquest cas hem definit una variable de tipus enter, number, per indicar la variable d’entrada. Podríem escriure que number ha de ser un enter positiu però estaríem utilitzant el llenguatge natural, que volem evitar en l’especificació. Per tant escrivim:
{ Pre: number = NUMBER ʌ NUMBER > 0 }
Per què escrivim number = NUMBER? Hem de tenir en compte que number és una variable i que durant l’execució de l’algorisme pot canviar el seu valor. Ara be, quan escrivim la postcondició, ho farem fent referència al valor inicial de la variable number. La manera d’indicar el valor inicial és escrivint:
number = NUMBER
Amb aquesta expressió volem indicar que la variable number inicialment tindrà un valor que no sabem quin és, però que l’identifiquem amb el nom NUMBER. Podríem haver escrit un altre nom o valor, però normalment s’utilitza el mateix nom de la variable en majúscules per indicar el seu valor inicial.
Nom de l’algorisme: busquem un nom representatiu del que fa l’algorisme. Podríem posar en aquest cas:
sumaQuadrats
Postcondició: a la postcondició hem d’indicar quin ha de ser l’estat final de l’entorn. Ho fem indicant quin ha de ser el valor correcte de la variable de sortida, en aquest cas sum. Si utilitzem llenguatge natural diríem sum ha de ser la suma dels quadrats dels nombres enters des de 1 fins NUMBER. En llenguatge formal escrivim:
{ Post: 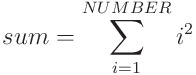 }
}
Cal fixar-se en que utilitzem NUMBER per indicar fins on hem de sumar. No podem utilitzar el nom de la variable number perquè durant l’execució pot haver canviat el seu valor.
Càlcul de predicats
A l’apartat anterior, hem indicat que les precondicions i postcondicions descriuen formalment i de manera no ambigua l’estat de l’entorn abans i després de l’execució d’un algorisme o un mètode, i hem vist un exemple de com fer-ho.
La pregunta és ara quin llenguatge cal utilitzar per especificar formalment. El llenguatge natural sabem que no sempre és l’adequat per escriure formalment les precondicions i postcondicions, ja que és fàcil introduir ambigüitat i pot ser difícil ser formal a l’hora d’escriure-les.
Una manera de fer-ho formalment és utilitzant el càlcul de predicats.
En aquest apartat recordem els components bàsics del càlcul de predicats que ens permeten escriure precondicions i postcondicions formals.
Recordem primer què és un predicat: és una expressió booleana en la que poden aparèixer variables.
Els següents son exemples de predicats vàlids:
- 3+6 > 15, que sempre té un valor fals, ja que 9 no és més gran que 15
- edat = 45, que pot tenir el valor cert o fals depenent del valor que tingui la variable edat. Si edat té el valor 45 el resultat serà cert, en cas contrari serà fals.
- edat*3 > 78, que pot tenir el valor cert o fals depenent del valor que tingui la variable edat. Si edat té el valor més gran que 26 el resultat serà cert, en cas contrari serà fals.
Un predicat pot estar format per:
- constants: 3, 89, 75, etc.
- variables: edat, any, dia, etc.
- operadors aritmètics:
| símbol | nom | es llegeix com |
| + | suma | més |
| - | resta | menys |
| * | multiplicació | per |
| / | divisió | dividit |
| div | divisió (part sencera) | part sencera de la divisió |
| mod | divisió (residu) | residu de la divisió |
| ∑ | sumatori | suma des de ... fins a ... |
- operadors relacionals:
| símbol | nom | es llegeix com |
| < | desigualtat | és menor que |
| ≤ | desigualtat | és menor o igual que |
| > | desigualtat | és major que |
| ≥ | desigualtat | és major o igual que |
| = | igualtat | és igual que |
| ≠ | desigualtat | és diferent que |
- operadors lògics:
| símbol | nom | es llegeix com |
| ʌ | conjunció lògica | i |
| v | disjunció lògica | o |
| ¬ | negació lògica | no |
| ⇒ | implicació en un sol sentit | llavors |
| ⇔ | doble implicació | si i només si |
- operadors de conjunts:
| símbol | nom | es llegeix com |
| {,} | delimitadors de conjunt | el conjunt format per |
| ∈ | pertinença de conjunts | pertany a |
| ∉ | pertinença de conjunts (negació) | no pertany a |
| ∪ | unió de conjunts | la unió de ... i ... |
| ∩ | intersecció de conjunts | la intersecció de ... i ... |
- quantificadors:
| símbol | nom | es llegeix com |
| ∀ | quantificador universal | per qualsevol |
| ∃ | quantificador existencial | existeix com a mínim |
| ∄ | quantificador existencial (negació) | no existeix cap |
| : | tal que |
- números:
| símbol | nom | es llegeix com |
| N | números naturals | N |
| Z | números enters | Z |
| Q | números racionals | Q |
| R | números reals | R |
| C | números complexes | C |
| √ | arrel quadrada | arrel de |
| ∞ | infinit | infinit |
| | | | valor absolut | valor absolut de |
| % | percentatge | percentatge de |
A continuació fem una breu explicació dels quantificadors, del seu significat i de la seva utilització.
Quantificador universal
El quantificador universal, escrit ∀, s’utilitza per indicar que tots els elements d’un conjunt compleixen una condició.
Exemple 02_02: si volem dir que per tot nombre real el seu quadrat també és real, escrivim:
∀x ∈ R ⇒ x*x ∈ R
Recordeu que el símbol ∈ es llegeix com pertany a. Per tant el predicat anterior es llegeix: per tot (∀) x que pertany als reals, el seu quadrat també pertany als reals.
Exemple 02_03: si volem dir que donats dos nombres reals menors que 1 el seu producte és un altre nombre real menor que 1 escrivim:
∀x,y ∈ R: x<1 ʌ y<1 ⇒ x*y < 1
Quantificador existencial
El quantificador existencial, escrit (∃) indica que al menys hi ha un element en un conjunt donat que compleix una condició.
Exemple 02_04: si volem escriure que donat un nombre real x positiu n’existeix un altre que és la seva arrel quadrada, escriuríem:
∀x ∈ R, ∃y ∈ R: y*y = x
Moltes vegades els quantificador es combinen en un mateix predicat. Veiem algun exemple:
Exemple 02_05: si volem escriure que entre dos nombres reals sempre n’hi ha un altre, escriuríem:
∀{x,z} ∈ R, ∃y ∈ R: x<z ⇒ x<y<z
Exemple 02_06: predicats amb quantificadors aplicats l’especificació
Suposem que volem especificar un mètode que calculi el màxim comú divisor de dos enters. Com ho escriuríem formalment?
Variables: necessitem dues variables per indicar l’entrada al mètode. Aquestes variables poden ser paràmetres d’una funció o acció:
var
x, y, mcd: integer;
end var
Precondició: cal indicar que tenim dos enters positius. Com ho fem? Escriuríem
{ Pre: x=X ʌ y=Y ʌ X>0 ʌ Y>0 }
Fixeu-vos que estem dient que el mètode ha de rebre dos enters que han de tenir un valor (no sabem quin i per tant ho indiquen amb X i Y) però que han de ser més grans que 0.
Nom de l'algorisme: en aquest cas podem anomenar-lo maxComunDivisor.
Postcondició: hem d’indicar que la variable mcd ha de ser un divisor de X i Y, i a més no n’hi pot haver cap altre més gran que result que compleixi la condició. Podem escriure:
{ Post: X mod mcd = 0 ʌ Y mod mcd = 0 ʌ ∀j ∈ N: j>mcd ʌ (X mod j ≠ 0 v Y mod j ≠ 0) }
A la postcondició diem que la variable result és divisor de X i de Y i a més, qualsevol enter més gran que result o no és divisor de X o no ho és de Y.
Especificació i programació
Encara que les precondicions serveixen per indicar quin són els valors vàlids d’entrada a un algorisme o mètode, i és responsabilitat del que executa l’algorisme entrar dades amb els valors adequats, sempre és aconsellable abans d’executar un algorisme o mètode, comprovar que es compleix la precondició. Si es detecta que la precondició no es compleix cal escriure un error i parar l’execució del programa.
Suposem que hem d’escriure un funció amb l’especificació de l’exemple de la suma de quadrats. És a dir una funció que, donat un enter positiu n retorni la suma del quadrats dels primers n enters. Caldria posar una comprovació de que el paràmetre actual passat en cridar a la funció no és negatiu. Si ho és, avortar el programa.
En C hi ha una funció que permet comprovar el valor d’una variable i en cas de que no compleixi la condició el programa es para. És la macro assert. Per utilitzar-la cal incloure la llibreria assert.h.
#include <assert.h>
Per comprovar que la variable number és més gran que 0 cal escriure dins del codi
assert(number > 0);
Si number té un valor negatiu o 0, el programa es pararà.
A l’exemple que ve a continuació podeu veure com s’escriuria:
[Exemple 02_07]
function squareAddition (number: integer): integer
var
sum: integer;
end var
{ Pre: number = NUMBER ʌ NUMBER > 0 }
if (number ≤ 0) then
{ stop program }
end if
{ Post: sum = ∑+(i=1)^NUMBER (i^2) }
{ ... }
end function
#include <assert.h>
int squareAddition(int number) {
int sum;
/* { Pre: number = NUMBER ʌ NUMBER >0 } */
assert(number >0)
/* { Post: sum = ∑+(i=1)^NUMBER (i^2) }
/* ... */
}
Les assercions normalment es poden activar o desactivar. En C, per desactivar-les cal incloure la directiva #define NDEBUG posada a l’inici del programa. Aquest directiva desactiva les assercions incloses en el programa. D’aquesta manera es poden incloure asserts en el programa mentre s’està desenvolupen i es poden desactivar quan el programa està provat.
Exemple 02_08
Problema: especificar un mètode que donat un import en euros que es pugui obtenir amb bitllets més grans o igual a 20€ calculi el mínim nombre de bitllets de cada tipus que són necessaris per aconseguir l’import indicat.
Per exemple, si tenim l'import 2.370€ el resultat esperat seria:
4 bitllets de 500€ 2.000
1 bitllet de 200€ 200
1 bitllet de 100€ 100
1 bitllet de 50€ 50
1 bitllet de 20€ 20
Total 2.370
I si tenim l'import 420€, el resultat seria:
2 bitllets de 200€ 200
1 bitllet de 20€ 20
Total 420
Especifiquem el mètode pas a pas:
Variables: el primer que hem de fer és identificar quines variable necessitem. En aquest cas necessitarem una variable de tipus enter per representar l’import d’entrada.
Pensem ara en quines necessitem per la sortida. Com hem de desglossar l’import en bitllets, necessitarem al menys una variable per cada tipus de bitllet, per indicar quants en necessitarem de cada tipus. Per tant escriurem el següent:
var
quantity: integer;
fiveHundred: integer;
twoHundred: integer;
oneHundred: integer;
fifties: integer;
twenties: integer;
end var
int quantity;
unsigned short fiveHundred;
unsigned short twoHundred;
unsigned short oneHundred;
unsigned short fifties;
unsigned short twenties;
Precondició: per escriure la precondició hem de pensar en que ha de ser cert respecte a la variable d’entrada, en aquest cas quantity. Ha de ser positiva i ha de ser múltiple de 20 o de 50 ja que no podem utilitzar els bitllets de 10. Per tan hem d’escriure:
{ Pre: quantity=QUANTITY ʌ QUANTITY>0 ʌ (QUANTITY mod 20 = 0 v QUANTITY mod 50 = 0) }
És a dir, diem que el valor inicial de quantity és representa amb QUANTITY, i aquest ha de ser positiu i a més ha de ser múltiple de 20 o de 50; la condició la validem mitjançant l'operador mod. Amb aquesta precondició, la quantitat 110 no seria acceptable, ni tampoc 20.010.
Nom de l'algorisme: podem escollir el nom que més ens agradi. Podríem dir-li per exemple divideixQuantity.
Postcondició: en la postcondició hem de dir com s’han de comportar les variables de sortida. El primer que podem dir és que la suma dels bitllets ens ha de donar l’import inicial. Tindríem doncs:
{ Post: QUANTITY = 500*fiveHundred + 200*twoHundred + 100*oneHundred + 50*fifties + 20*twenties }
Ara bé, el que hem escrit és suficient? És fàcil veure que la postcondició que hem donat compleix en el fet de que la quantitat final seria correcta, però no compleix la condició de que s’utilitzi el mínim de bitllets possible. Per exemple, 420 el podríem representar amb 21 bitllets de 20, però no seria la solució que es busca.
Per tant cal posar una condició més restrictiva. Per fer-ho hem de pensar en el nombre màxim de bitllets de cada tipus:
- De 500 podem tenir qualsevol nombre.
- De 200 només en podem tenir 2 per sumar fins a 400, ja que 3 sumarien 600 que es pot representar amb un de 500 i un de 100.
- De 100 nomé n’hi pot haver 1.
- De 50 només n’hi pot haver 1.
- De 20 n’hi pot haver fins a 4.
Per tant, si volem escriure la postcondició complerta cal escriure:
{ Post: (QUANTITY = 500*fiveHundred + 200*twoHundred + 100*oneHundred + 50*fifties + 20*twenties) ʌ
(0 ≤ fiveHundred ) ʌ (0 ≤ twoHundred ≤ 2) ʌ (0 ≤ oneHundred ≤ 1) ʌ (0 ≤ fifties ≤ 1) ʌ (0 ≤ twenties ≤ 4) }
Resum
En aquesta unitat hem vist com especificar un problema de manera formal.
- S'han definit els elements de l'especificació
- S'han introduït els elements bàsics del càlcul de predicats que ens permeten especificar els problemes d'una manera formal
- S'ha vist un exemple en detall per veure com definir una especificació