Introducció

Com ja s'ha comentat en el mòdul Introducció a la Complexitat és necessari establir un criteri per decidir entre diversos algorismes que resolen un mateix problema.

Amb aquest objectiu analitzem l'eficiència d'un algorisme sobre la base del seu temps d'execució. El temps d'execució d'un algorisme ens determina la seva complexitat, és a dir la velocitat de creixement del temps d'execució en augmentar la mida de l'entrada.

En aquest mòdul analitzarem com calcular el temps d'execució d'un algorisme amb l'objectiu de determinar la seva complexitat.

Repàs de notació asimptòtica

En el mòdul de Introducció a la Complexitat s'ha comentat que l'eficiència d'un algorisme depèn del seu temps d'execució, T( n ). A aquest temps se'l pot descriure amb una funció f( n ), que ens indica que T( n ) és proporcional a f( n ). Es va comentar també que la notació asimptòtica ens serveix per indicar la velocitat de creixement d'una funció del temps d'execució d'un algorisme. Diem que T( n ) és O(f( n )) quan la velocitat de creixement de T( n ) està fitada superiorment per f( n ). Així O(f( n )) representa el conjunt de totes les funcions g( n ) que creixen com a molt tan ràpidament com a f( n ).

Exemple 10_01 : el conjunt de funcions O(20n³) és el mateix que O(n³).

Solució : a partir de la definició de O( f ) queda clar que les constants no tenen cap efecte en la notació asimptòtica, i per tant poden ser ignorades. En aquest cas si la constant c = 20, totes les funcions dins de O(20n³) també están dins de O(n³).

Exemple 10_02 : el conjunt de funcions O(20n³ + 40n² + 80n) és el mateix que O(n³).

Solució : segons la definició asimptòtica, afegir termes a f amb una velocitat de creixement menor no afecta al conjunt de funcions que forma part de O(f( n )). És a dir que si g( n ) ∈ O(f( n )) llavors  O(f( n )+g( n )) = O(f( n )).

Exemple 10_03 : Regla de la suma : P₁ i P₂ dos algorismes amb temps d'execució T₁( n ) i T₂( n ) respectivament, que són O(f( n )) i O(g( n )). Si P₁ i P₂ se executen seqüencialment, llavors la complexitat de su composició és O(max(f( n ), g( n ))).

Solució : T₁( n ) + T₂( n ) tindrà complexitat O(max(f( n ), g( n ))). Això últim ve del fet que correspon a la velocitat de creixement major segons s'ha vist en un cas d'estudi anterior.

Exemple 10_04 : Regla del producte: P₁ i P₂ dos algorismes amb temps d'execució T₁( n ) i T₂( n ) respectivament, són O(f( n )) i O(g( n )).

Solució : el temps resultat del producte T₁( n ) . T₂( n ) té complexitat igual a la complexitat del producte de les funcions: O(f( n ) . g( n )).

Exemple 10_05 : de les regles del producte i la suma es deriva:

• Si T( n ) = c llavors T( n ) = O(1).
• Si T( n ) = c + f( n ) llavors T( n ) = O(f( n )).
• Si T( n ) = c . f( n ) llavors T( n ) = O(f( n )).

Anàlisi d'algorismes

Quan s'analitza un algorisme el que es fa és analitzar la complexitat de cadascuna de les seves parts, i després calcular la complexitat resultat de la seva composició. En general els algorismes acostumen a estar compostos per parts seqüencials i parts iteratives.

A continuació veurem la complexitat per als tipus de sentències més habituals d'un algorisme.

Assignació

L'assignació te temps constant per tant té ordre de complexitat O(1).

Exemple 10_06 :

    a := 100;
    a := a + 1;
    a := (b div 4) mod 8 + 1000;

Seqüència d'instruccions

Donada la seqüència d'instruccions: P₁;P₂;..;P_k con T_i( n ) = O(f_i( n )) respectivament, la complexitat de la seqüència està donada per l'expressió:

        k

    ∑ T_i ( n ) = O(max{f₁( n ), f₂( n ), .., f_k( n )})

    i = 1

Sentència condicional

Donada la següent forma de sentència condicional:

   if <condició> then <instruccions> end if

El temps d'execució d'aquesta sentència está donat pel temps de <condició> que anomenarem T₁( n ), sumat al temps de <instruccions> (seria el pitjor cas) que anomenarem T₂( n ). Per la regla de la suma, si T₁( n ) té ordre de complexitat  O(f( n )) i T₂( n ) té ordre de complexitat O(g( n )), llavors el temps de la sentència condicional és T1( n ) + T2( n ) i l'ordre de complexitat és O(max{f( n ),g( n )}.

Per a una sentència condicional de la forma:

   if <condició> then <instruccions1> else <instruccions2> end if

El temps d'execució d'aquesta sentència està donat pel temps de <condició> que anomenarem T₁( n ), sumat al màxim dels temps d'execució (seria el pitjor cas) de <instrucccions1> i de <instruccions2> que anomenarem T₂( n ) i T₃( n ) respectivament.

Si T₁( n ), T₂( n ), T₃( n ) tenen ordre de complexitat O(f( n )), O(g( n )) i O(h( n )) respectivament, llavors la complexitat de l'expressió T₁( n ) + max{T₂( n ),T₃( n )}, per la regla de la suma, està donada per O(max{f( n ), max{g( n ), h( n )}}, o sinó més senzillament per O(max{f( n ), g( n ), h( n )}).

Exemple 10_07 :

Donat el següent troç de codi:

1    if (a > 0) then

2            b := a;

3    else

4      b := a + b - 48*(a%1003);

5        end if

Calcular el temps d'execució i la seva complexitat:

El temps d'execució T( n ) = T₁( n ) + max{T₂( n ), T₄( n )}, sent T₁, T₂ i T₄ els temps d'execució de les línies 1, 2 i 4 respectivament. Donat que la comparació i l'assignació tenen complexitat constant, tenim que:

T( n ) = k₁ + max{k₂, k₄} = k, per tant l'ordre de complexitat és constant (O(1)).

Sentència iterativa

El temps d'execució d'una sentència iterativa que executa k iteracions està donat per la suma del temps d'avaluar la condició k+1 vegades, sumat al temps d'executar cada iteració k vegades.

Per a una sentència iterativa de la forma:

while <condició> do <instruccions> end while

El temps d'execució d'aquesta sentència està donat pel temps de <condició> que anomenarem T₁( n ), sumat al temps del bucle. Si <instruccions> amb temps d'execució T₂( n ), s'executa k vegades, tenim que el temps d'execució de la sentència iterativa està donada per l'expressió:

                                    k

  T( n ) = T₁( n ) + ∑ (T₁( n ) + T₂ ( n )) = T₁( n ) + k .(T₁( n ) + T₂( n ))

                                i=1

Exemple 10_08 :

Donat el següent tros de codi calcula el temps d'execució i la seva complexitat:

1      i := 1;

2            count := 0;

3      while (i ≤ n) do

4            if (v[i] = x) then

5                 count := count + 1;

6            end if

7            i := i + 1;

8      end while

En una seqüència d'instruccions, el temps total està donat per la suma dels temps de cada instrucció. Si T₁ ( n ) i T₂ ( n ) corresponen al temps d'execució de les línies 1 i 2 respectivament, i T_3-8( n ) al temps d'execució del bucle, el temps total està donat per l'expressió:

T( n ) = T₁( n ) + T₂( n ) + T_3-8( n )

Les assignacions tenen temp contante, per tant T₁( n ) =  k₁ i T₂( n ) = k₂.

El temps d'execució de les instruccions del bucle:

El temps d'una sentència condicional està donat pel temps de la condició T₄( n ) (linia 4) sumat al temps de les instruccions de la sentència condicional (pitjor cas), T₅( n ) (linia 5).

Si T₃( n ) és el temps d'execució de la condició del bucle (linia 3) i T₇( n ) és el temps de la linia 7, tenim que el temps d'execució de cada iteració del bucle està donat per l'expressió T₃( n ) + T₄( n ) + T₅( n ) + T₇( n ).

Per tant, si el nombre d'iteracions totals és n, tenim que el temps d'execució del bucle és:

 T_3-8( n ) = T₃( n ) + n . (T₃( n ) + T₄( n ) +  T₅( n ) + T₇( n ))

Donat que les assignacions i comparacions tenen temps constants:

  T_3-8( n ) = k₃ + n . ( k_{3 +} k₄ + k₅ + k₇)

El temps total del tros de codi de l'exemple és:

 T( n ) = k₁ + k₂ + k₃ + n . ( k_{3 +} k₄ + k₅ + k₇) = k + n.k  i això té complexitat lineal O( n ).

Anàlisi de recurrència

Per realitzar l'anàlisi d'algorismes recursivos es procedeix igual que amb els algorismes no recursivos: es calcula primer la seva funció del temps d'execució i després s'expressa aquesta funció en notació asimptòtica.

La definició del temps d'execució T( n ) d'un algorisme recursiu està en funció dels temps d'execució de cada invocació recursiva, és a dir de si mateixa, per la qual cosa aquesta funció és recurrent.

La resolució d'equacions recurrents, pot ser bastant complexa. Un mètode per resoldre aquest tipus d'execucions consisteix en aplicar la definició recurrent de forma repetida fins que es pugui aplicar el cas base, és a dir la part no recurrent de la definició.

Exemple 10_09 :

Resoldre l'equació següent (exemple tret de [1]):

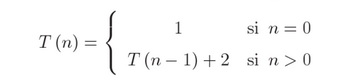
Resoldre aquesta equació significa obtenir una expressió per a T( n ) que no estigui en funció de si mateixa sinó de n.

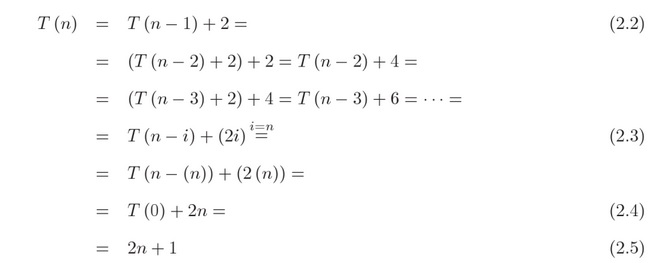
El mètode consisteix en reescriure la definició recursiva (2.2) i a continuació substituir T( n-1 ) per la definició recursiva, però en funció ara de n-1. Aquest pas es repeteix diverses vegades fins a fer-ho genèric per a i vegades (2.3). Arribat aquest punt és necessari trobar el valor que ha de tenir i per tal de convertir l'expressió genèrica en el cas base. En aquest exemple, el cas base succeeix quan n = 0, per tant per convertir el cas genèric en el cas base, tenim que i ha de ser i = n. D'aquesta forma arribem primer a (2.4) i donat que T( 0 ) = 1 per definició de la funció, arribem a (2.5). Per tant T( n ) = 2n + 1.

Exemple 10_10 :

Calcular la complexitat computacional de l'acció replace.

Per analitzar la complexitat computacional d'aquesta acció, cal observar que en cada crida el valor del paràmetre size disminueix en una unitat i quan arriba a 0 llavors finalitza la recursivitat. Per tant, la funció de temps cal definir-la en funció de n = size.

Així doncs, podem definir la funció de temps de la següent manera:

Resolem la recurrència repetint la substitució recursiva un total de i vegades:

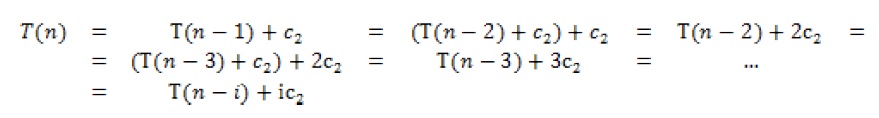
Calculem el valor de la variable i que fa que es pugui aplicar la part no recurrent de la definició de T( n ):

    n - i = 0
    n = i

Finalitzem el càlcul de T( n ) amb el valor calculat per a la variable i:

La conclusió és que l'acció replace té complexitat lineal O( n ), on n és el valor del paràmetre size.

Exemple 10_11 :

Calcular la complexitat computacional de la funció sumCount. Es pot assumir que el nombre màxim d'elements de la llista de cada entrada de la taula coincideix amb la mida del vector (N). La funció de temps de countNeg es T_c( n ) = k₁ + n·k₂ que té complexitat computacional lineal (O( n )) sent n el nombre d'elements de la llista en el pitjor cas.

Per analitzar la complexitat de sumCount és necessari plantejar la seva funció de temps, la qual calcularem en funció de la mida del vector d'entrada, m i que denominarem T_s( m ). Considerarem el pitjor cas que és quan el nombre d'elements (nelem) és igual a m. Per tant la funció de temps de sumCount es pot plantejar com segueix:

T_s( m ) = k₃ , si m = 0
T_s( m ) = k₄ + T_c( n ) + T_s( m-1 ) , si m > 0

El cas base consta d'una comparació i una assignació. Donat que ambdues són operacions elementals, llavors té un cost de temps constant que anomenarem k₃.

El cas recursiu consta d'una assignació i una suma amb temps constant k₄, una invocació a la funció countNeg amb temps donat per la funció T_c i una invocació recursiva a sumCount. Per tant la funció de temps per calcular el cost de la crida recursiva és:

T_s( m ) = k₄ + T_c( n ) + T_s( m-1 ) = k₄ + T_c( n ) + (k₄ + T_c( n ) + T_s( m-1-1 )) =
  = k₄ + k₄ + T_c( n ) + T_c( n ) + T_s( m-1-1 ) = 2k₄ + 2T_c( n ) + T_s( m-2 ) =
  = 2k₄ + 2T_c( n ) + (k₄ + T_c( n ) +T_s( m-2-1 )) = 3k₄ + 3T_c( n ) + T_s( m-3 ) =
  = … =
  = i·k₄ + i·T_c( n ) + T_s( m-i )

Per poder aplicar el cas base, m ha de ser igual a i, ja que volem T_s(0). Completem el càlcul amb i = m i apliquem el cas base:

T_s( m ) = m·k₄ + m·T_c( n ) + T_s( m-m ) = m·k₄ + m· T_c( n ) + T( 0 ) =
  = m·k₄ + m·T_c( n ) + k₃

Donat que el nombre elements de la funció de temps T_c( n ) en el pitjor cas coincideix amb la mida del vector, podem utilitzar n en lloc de m. Per tant, podem reescriure la funció de temps T_s( n ) de sumCount com:

T_s( n ) = n·k₄ + n·(k₁ + n·k₂) + k₃ = k₃ + n·(k₁ + k₄) + n² ·k₂ = O(n²)

Podem dir que la funció sumCount té una complexitat quadràtica, O(n²) sent n el nombre d'elements en el vector d'entrada.

Resum

En aquest mòdul s'ha repassat la notació asimptòtica i s'han donat els conceptes bàsics per a l'anàlisi d'algorismes. S'ha introduït el càlcul de la funció de temps per a tipus de sentències comunes com: assignació, sentència condicional, sentència iterativa. I s'ha calculat a partir de la funció de temps la seva complexitat.

Finalment s'ha vist anàlisi d'algorismes recurrents i un mètode per calcular la seva funció de temps.

Bibliografia

[1] Manual d'algorísmica: Recursivitat, complexitat i disseny d'algorismes . Jesús Bisbal Riera