Vectors i matrius
Objectius
- Entendre el concepte de vector i matriu.
- Indexació en vectors i matrius.
- Representació a memòria dels vectors i les matrius.
Introducció
Fins ara hem vist que les variables són objectes que poden contenir valors de diferents tipus, com per exemple enters, reals o caràcters. En aquesta unitat veurem que podem definir variables que contenen diversos elements d’un mateix tipus. Segons aquestes variables tinguin 1 o 2 dimensions, les anomenarem vectors o matrius respectivament. També veurem com podem accedir a cadascun dels elements d’un vector o d’una matriu, i com aquests queden emmagatzemats en memòria.
1. Vectors
Els vectors, o arrays en anglès, són estructures d’una sola dimensió, que poden emmagatzemar n valors d’un mateix tipus. Per exemple, imagineu que volem guardar les temperatures màximes de cada dia de la setmana. Amb el que hem vist fins ara, hauríem de definir set variables, una per a cada dia:
var
t1, t2, t3, t4, t5, t6, t7: real;
end var
float t1,t2,t3,t4,t5,t6,t7;
Si ho definim en forma de vector, podem crear un objecte que pugui guardar els set valors:
var
t : vector[7] of real;
end var
float t[7];
Per a accedir a l’enèsima posició d’un vector ho farem amb [n], on n és la posició a la qual volem accedir, per exemple, t[3]. Un punt molt important que cal tenir en compte quan treballem amb vectors és quin valor té la primera posició. En alguns llenguatges, la primera posició té un valor 0, per tant, t[0] seria la primera temperatura, mentre que en altres llenguatges, es considera que la primera posició té valor 1 i, per tant, per a obtenir la primera temperatura hauríem d’escriure t[1]. Quan treballem amb llenguatge algorísmic utilitzem com a primera posició la 1, ja que en notació matemàtica, la primera posició d’un vector és aquesta. Quan treballem amb llenguatge C, la primera posició serà sempre 0.
Per tant, l’expressió per a calcular la temperatura mitjana seria:
(t[1] + t[2] + t[3] + t[4] + t[5] + t[6] + t[7]) / 7.0;
Si ho posem tot junt en un algorisme que ens demani les temperatures i ens mostri la temperatura mitjana, tindrem el següent:
[Exemple 08_01]
algorithm tempAverage
var
t: vector[7] of real;
m: real;
end var
t[1] := readReal();
t[2] := readReal();
t[3] := readReal();
t[4] := readReal();
t[5] := readReal();
t[6] := readReal();
t[7] := readReal();
m:=(t[1] + t[2] + t[3] + t[4] + t[5] + t[6] + t[7]) /7.0;
writeReal(m);
end algorithm
int main(int argc, char** argv) {
float t[7];
float m;
scanf("%f %f %f %f %f %f %f", &(t[0]), &(t[1]), &(t[2]), &(t[3]), &(t[4]), &(t[5]), &(t[6]));
m=(t[0] + t[1] + t[2] + t[3] + t[4] + t[5] + t[6]) / 7;
printf("%f", m);
return 0;
}
Atès que quan es carrega un programa per a la seva execució es reserva la memòria per a les seves variables i entre elles els vectors, quan definim un vector podem utilitzar constants per a la seva dimensió, però mai variables, ja que aquestes no tenen un valor conegut fins que ja s’està executant el programa. Per tant, podem fer:
#define N 3
int main(int argc, char** argv) {
float v[N];
}
Però no podem fer:
int main(int argc, char** argv) {
int m=3;
float v[m];
}
Quan la longitud d’un vector és una dada del problema, és una bona pràctica definir-la com una constant, ja que ens permet modificar aquesta dada ràpidament. Per exemple, si en el cas de les temperatures setmanals les volguéssim canviar perquè fossin anuals, caldria canviar el nombre de posicions 7 per 365, i en el càlcul de la mitjana també caldria dividir per 365 en comptes de 7. Si ho tinguéssim definit a partir d’una constant, solament caldria canviar la constant.
1.1. Cadenes de caràcters o strings
Un tipus molt utilitzat de vector són les cadenes de caràcters, sovint conegudes pel seu nom en anglès strings. En C, per a definir una cadena de caràcters ho farem com un vector normal, però cal tenir en compte que les cadenes de caràcters, per a poder ser interpretades com a tals, han de finalitzar sempre amb el caràcter (‘\0’), que té valor ASCII 0. Per tant, si volem guardar una cadena de caràcters caldrà reservar memòria per a una posició addicional.
En llenguatge algorísmic generalment no es declara com a vector sinó com a cadena de caràcters. A continuació es mostra un exemple:
[Exemple 08_02]
algorithm sayHello
var
name: string;
end var
writeString("What's your name?");
name := readString();
writeString("Hello" + name);
end algorithm
#define MAX_NAME_LEN 25
int main(int argc, char** argv) {
char name[MAX_NAME_LEN];
printf("What's your name?\n");
scanf("%s", name);
printf("Hello %s\n", name);
return 0;
}
Fixeu-vos que en el cas de les cadenes de caràcters, quan utilitzem la instrucció en C scanf no posem el símbol & davant.
1.2. Representació en memòria
Totes les posicions d’un vector es guarden en memòria consecutivament i, per tant, un vector de n posicions ocuparà n vegades el que ocupa el seu tipus bàsic. Per exemple, si tenim un vector d’enters a, i un enter ocupa 4 bytes en memòria de manera que ocupa fins a la posició X, el vector de 4 enters ocuparà 4x4 = 16 bytes en memòria:

La representació gràfica de com queda en memòria una variable és una eina molt útil per a fer el seguiment del programa. A aquest efecte, podem posar en ordre invers les posicions, suposar que la posició inicial és 0 i agrupar els bytes que contenen un valor del vector. Per exemple, si el vector conté els valors {1, 4, -1, 1023}, el podem representar com:

1.3 Inicialització
Igual que una variable de tipus bàsic, els vectors també es poden inicialitzar quan els definim. En aquest cas utilitzarem les claus ({ i }) per a indicar que és un vector. Quan inicialitzem un vector, no és obligatori definir la seva longitud, ja que s’obté a partir del nombre d’elements donats. Per exemple:
[Exemple 08_03]
var
v1 : vector[3] of integer:={3, 5, -1} ;
v2 : vector of integer:={3, 5, -1} ;
v3 : vector[4] of integer:={3, 5, -1} ;
end var
/* Variable definition*/
int v1[3] = {3, 5, -1};
int v2[] = {3, 5, -1};
int v3[4] = {3, 5, -1};
En C, tingueu en compte que v2 no té especificada la longitud, i per tant es definirà com un vector d’enters amb 3 posicions. En el cas de v3, és un vector de 4 posicions del que solament inicialitzem les 3 primeres.
En el cas de les cadenes de caràcters, podem utilitzar les cometes dobles ("), o tractar-ho igual que un vector normal i assignar caràcter a caràcter. A continuació es mostra un exemple de codi on s’inicialitzen les cadenes de caràcters de diferents formes i es mostra per a cada variable el seu contingut i la mida en bytes. Tingueu en compte que quan utilitzem les cometes dobles s’afegeix el símbol de final de cadena (‘\0’) automàticament.
[Exemple 08_04]
int main() {
char a[] = {'a','b','c','\0'};
char b[4] = {'a','b','c','\0'};
char c[] = "abc";
char d[4] = "abc";
printf("a - %s --> (%d) bytes\n", a, sizeof(a));
printf("b - %s --> (%d) bytes\n", b, sizeof(b));
printf("c - %s --> (%d) bytes\n", c, sizeof(c));
printf("d - %s --> (%d) bytes\n", d, sizeof(d));
return 0;
}
2. Matrius
Les matrius són vectors de dues dimensions. Per exemple, per a definir la matriu:
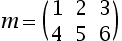
Ho podem fer de la manera següent:
var
m : matrix[2][3] of integer:={{1, 2, 3}, {4, 5, 6}} ;
end var
/* Variable definition*/
int m[2][3] = {{1, 2, 3}, {4, 5, 6}};
Tingueu en compte que primer es declara el nombre de files i després el de columnes. Igual que en el cas dels vectors, cal tenir en compte que els índexs de les posicions poden començar en 0 o en 1. A continuació es mostra un exemple en el qual es calcula el valor mitjana de tots els valors de la matriu anterior.
[Exemple 08_05]
algorithm matAverage
var
m : matrix[2][3] of integer:={{1, 2, 3}, {4, 5, 6}} ;
r : real;
end var
r:=integerToReal(m[1][1] + m[1][2] + m[1][3] + m[2][1] + m[2][2] + m[2][3]);
r:= r/6;
writeReal(r);
end algorithm
int main() {
/* Variable definition*/
int m[2][3] = {{1, 2, 3}, {4, 5, 6}};
float r;
r=(m[0][0] + m[0][1] + m[0][2] + m[1][0] + m[1][1] + m[1][2])/6.0;
printf("%f\n", r);
return 0;
}
Quan es guarda en memòria, es fa per files. Per tant, una matriu com l’anterior en memòria és equivalent a un vector de 2x3 = 6 posicions i per tant de 6x4 = 24 bytes.

3. Exemples
3.1. Exemple 08_06
Definir un algorisme que calculi el producte escalar de dos vectors en un espai de dues dimensions (2D).
algorithm dotProduct
var
a : vector[2] of integer;
b : vector[2] of integer;
c : integer;
end var
a[1] := readInteger();
a[2] := readInteger();
b[1] := readInteger();
b[2] := readInteger();
c:= a[1] * b[1] + a[2] * b[2];
writeInteger(c);
end algorithm
int main() {
/* Variable definition*/
int a[2], b[2];
int c;
scanf("%d %d %d %d", &(a[0]), &(a[1]), &(b[0]), &(b[1]));
c=a[0] * b[0] + a[1] * b[1];
printf("(%d,%d) * (%d,%d) = %d\n", a[0], a[1], b[0], b[1], c);
return 0;
}
3.2. Exemple 08_07
Definir un algorisme que calculi el producte entre la matriu identitat de 3x3 i un valor enter introduït per teclat.
algorithm dotProduct
var
id : matrix[3][3] of integer := {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
s : integer;
r : matrix[3][3] of integer;
end var
s := readInteger();
r[1][1]:= id[[1][1] * s;
r[1][2]:= id[[1][2] * s;
r[1][3]:= id[[1][3] * s;
r[2][1]:= id[[2][1] * s;
r[2][2]:= id[[2][2] * s;
r[2][3]:= id[[2][3] * s;
r[3][1]:= id[[3][1] * s;
r[3][2]:= id[[3][2] * s;
r[3][3]:= id[[3][3] * s;
end algorithm
int main() {
/* Variable definition*/
int id[3][3]={{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
int s;
int r[3][3];
scanf("%d", &s);
r[0][0]= id[[0][0] * s;
r[0][1]= id[[0][1] * s;
r[0][2]= id[[0][2] * s;
r[1][0]= id[[1][0] * s;
r[1][1]= id[[1][1] * s;
r[1][2]= id[[1][2] * s;
r[2][0]= id[[2][0] * s;
r[2][1]= id[[2][1] * s;
r[2][2]= id[[2][2] * s;
return 0;
}
Resum
En aquesta unitat hem vist com definir i inicialitzar vectors i matrius, tant en llenguatge algorísmic com en els llenguatges de programació. També hem vist com accedir als valors d’un vector i matriu tant per a utilitzar-los com per a assignar nous valors. A més hem vist que les cadenes de caràcter són un vector amb algunes propietats que cal tenir en compte quan programem en llenguatge C.