Modularitat
Objectius
- Entendre la utilitat de les accions i funcions.
- Comprendre la diferència entre acció i funció.
- Entendre que és un paràmetre actual i distingir-lo del paràmetre formal.
- Saber definir accions i funcions i saber-les cridar.
- Distingir entre les implicacions de passar paràmetres d’entrada a passar-los de sortida.
- Comprendre el concepte de modularització dels algorismes.
Introducció
Els algorismes que hem vist fins al moment han estat algorismes senzills on s’han utilitzat assignacions i estructures de control tant alternatives (pera prendre decisions) com iteratives (per a repetir accions fins que es compleixi una condició).
Aquestes estructures ens permeten escriure algorismes simples, però quan els algorismes es compliquen, l’escriptura d’un algorisme seqüencial i la seva posterior comprensió i manteniment es poden complicar molt.
1. Aproximació intuïtiva
Pensem, per exemple, en un menjar que vulguem fer a casa. Tenim dues opcions, fer una per una totes les tasques necessàries per a cuinar tot el que ens cal, o bé podem encarregar a diferents especialistes els diferents plats que necessitem.
Si volem fer un algorisme de preparació del menú, en el cas de fer-ho tot nosaltres hauríem d’especificar tots els passos per a cuinar tots els plats. Tindríem un algorisme llarg que descriuria l’elaboració de cada plat. En canvi, si agafem la segona opció, l’algorisme quedaria bastant més senzill.
Suposem, per exemple, que el menú que volem consisteix en paella, bacallà amb allioli i pastís. Si optem per la segona via, l’algorisme podria quedar més o menys com segueix:
[Exemple 14_01]
algorithm dinar
var
primerPlat, salsa, segonPlat, postres: tPlat;
end var
primerPlat:= encarregaPaella(marisc, 5);
segonPlat:= encarregaPeix(bacallà, all_i_oli, 5);
postres:= encarregaPostres(pastis, xocolata, espelmes, 5);
end algorithm
Comentaris:
- Hem suposat que tPlat és un tipus de variable del nostre entorn de definició d’algorismes de cuina.
- Per a demanar cadascun dels plats, hem posat entre parèntesis les indicacions de com volem el plat. Marisc i 5 per a la paella per a indicar que la volem de marisc i per a cinc persones. Bacallà, allioli i 5 per a indicar el tipus de peix, la salsa i el nombre de persones, i el mateix per a les postres.
- L’especialista ha determinat les opcions que hem de triar i nosaltres hem de donar valor a aquestes opcions en fer l’encàrrec. Els cuiners de paella només ens deixen triar el tipus de paella i els comensals. Els subministradors de plats de peix, en canvi, a més de les persones i el tipus de peix també ens permeten triar una salsa. El pastisser deixa més opcions a decidir a qui fa l’encàrrec.
Perquè puguem utilitzar un especialista hem de saber quines dades comunicar-li per a fer un encàrrec correcte.
Podem veure com el nostre algorisme, a força de sol·licitar experts que facin la feina, es converteix en un algorisme simple i fàcil d’entendre. L’única cosa que hem hagut de fer són peticions en les quals hem afegit valors, als quals anomenem paràmetres, que indiquen exactament com volem cada plat.
A més, amb aquest sistema, la recepta (algorisme) exacta que hi ha darrere de cada plat, mentre compleixi amb el que s’espera, ens és igual quina sigui. Si algun cuiner decideix canviar la recepta, per a millorar-la, ens és igual sempre que el resultat es mantingui.
Els llenguatges de programació permeten treballar d’una manera similar a com ho hem fet en el nostre menú. És a dir, es poden utilitzar subalgorismes, o se’n poden definir altres de nous, que queden a part de l’algorisme principal i que permeten dividir un algorisme complicat en subalgorismes més simples. A més, com veurem als següents apartats, un altre dels avantatges que proporcionen és el fet que aquests subalgorismes es poden reutilitzar per evitar la reescriptura de codi.
Aquests subalgorismes reben el nom d’accions i funcions i és com si empaquetéssim un conjunt d’instruccions que resolen un problema i no ens hem de preocupar del que hi ha dins.
De fet, en les unitats anteriors ja s’han utilitzat. Per exemple,
- En llegir o escriure dades. La lectura i escriptura de dades ha d’utilitzar crides al sistema operatiu, que és com interactua el programa amb l’ordinador en concret que estem utilitzant. Per a poder escriure algorismes que no depenguin del SO, els llenguatges de programació ofereixen accions o funcions per a realitzar aquesta tasca. Ens n’independitzen. Per exemple, hem utilitzat:
- En llenguatge algorísmic hem usat i=readInteger() i en C scanf("%d", &i) per a llegir un nombre enter.
Podeu veure l’apartat d’accions i funcions predefinides per a veure una llista d’algunes de les accions i funcions més comunes que ja venen definides amb els llenguatges de programació.
- O, per exemple, quan s’ha utilitzat switchOnAirConditioning() en la unitat de l’estructura alternativa, on es dona per suposat que hi ha un subalgorisme que realitza l’acció d’encendre l’aire condicionat.
Vegem amb un exemple com podem millorar un algorisme usant aquest concepte.
1.1. Exemple - Càlcul de combinacions
Suposem que hem de dissenyar un algorisme que permeti saber quantes combinacions de colors es poden fer si disposem de n teles, cadascuna d’un color diferent. Concretament es vol disposar d’un algorisme genèric que donats n colors calculi quantes combinacions es poden fer utilitzant cada vegada m colors, on m i n són enters i m ≤ n.
Recordem que la fórmula matemàtica per a calcular les combinacions ve donada pel nombre combinatori i que es calcula de la manera següent:
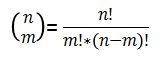
Dissenyem primer la solució sense preocupar-nos del càlcul del factorial, que ja hem vist en la unitat d’estructures iteratives.
Per a dissenyar l’algorisme haurem de llegir els valors de n i m i haver-ho indicat a la fórmula. Quedaria:
[Exemple 14_02]
algorithm combinations
var
{definim les variables, dos enters que cal llegir i una on emmagatzemar el resultat}
totalNumColors, colorsToCombine: integer;
result: integer;
end var
{llegim els 2 nombres}
totalNumColors:= readInteger();
colorsToCombine:= readInteger();
{fem un primer esbós del càlcul, suposant que tenim una manera de calcular el factorial d’un nombre}
result := totalNumColors! div (colorsToCombine! * (totalNumColors - colorsToCombine)!);
writeInteger(result);
end algorithm
int main() {
int totalNumColors;
int colorsToCombine;
int result;
result = totalNumColors! / (colorsToCombine! * (totalNumColors - colorsToCombine)!) ;
printf ("%d ", result);
return 0;
}
Com podem veure, si suposem que tenim una manera de calcular el factorial, ens queda un disseny simple i fàcil d’entendre.
Ara bé, com hem vist prèviament, el càlcul del factorial no és tan simple com una sola línia de codi. Per a calcular-lo cal fer una iteració per anar calculant el producte de tots els enters, a més de la necessitat de variables on guardar els càlculs parcials. Recordem com es calculava:
[Exemple 14_03]
var
factorial: integer;
i: integer;
n: integer;
end var
n:= readInteger();
factorial:= 1;
i:=1;
while i ≤ n do
factorial := factorial * i;
i := i + 1;
end while
int main() {
int factorial;
int i;
int n;
scanf("%d", &n);
factorial = 1;
i = 1;
while( i <= n) {
factorial = factorial * i;
i++;
}
return 0;
}
Si incorporem el càlcul del factorial al nostre algorisme veiem que per a calcular-lo necessitem diverses línies de codi que, a més, s’han de repetir tres vegades per a calcular cadascun dels factorials. L’algorisme quedaria:
[Exemple 14_04]
algorithm combinations
var
{definim les variables, dos enters que cal llegir i una on emmagatzemar el resultat a més d'altres auxiliars}
totalNumColors, colorsToCombine: integer;
factorial1: integer;
factorial2: integer;
factorial3: integer;
i: integer;
result: integer;
end var
{llegim els 2 nombres}
totalNumColors:= readInteger();
colorsToCombine:= readInteger();
{calculem els factorials}
factorial1 := 1;
i:=1;
while (i ≤ totalNumColors) do
factorial1 := factorial1*i;
i := i + 1;
end while
factorial2 := 1;
i := 1;
while (i ≤ colorsToCombine) do
factorial2 := factorial2 * i;
i := i + 1;
end while
factorial3 := 1;
i := 1;
while (i ≤ (totalColorsToCombine - colorsToCombine)) do
factorial3: = factorial3*i;
i := i+1;
end while
result := factorial1 div (factorial2 * factorial3) ;
writeInteger(result);
end algorithm
int main() {
/*declare variables, two read integer and one result integer*/
int totalNumColors, colorsToCombine;
int factorial1;
int factorial2;
int factorial3;
int i;
int result;
/*get two numbers*/
scanf("%d %d", &totalNumColors, &colorsToCombine);
/*compute factorials*/
factorial1 = 1;
i = 1;
while(i <= totalNumColors) {
factorial1 = factorial1 * i;
i++;
}
factorial2 = 1;
i = 1;
while (i <= colorsToCombine) {
factorial2 = factorial2 * i;
i++;
}
factorial3 = 1;
i = 1;
while (i <= totalNumColors - colorsToCombine) {
factorial3 = factorial3 * i;
i++;
}
result = factorial1 / (factorial2 * factorial3) ;
printf("%d ", result);
return 0;
}
Per tant, escriure l’algorisme complet solament amb els elements bàsics del llenguatge algorísmic implica que un disseny aparentment simple es compliqui per haver de substituir, com a passa en el nostre exemple, una divisió per moltes línies de codi que són, a més, repetitives.
En canvi, si dissenyem un subalgorisme que calculi el factorial i que puguem usar passant-li un paràmetre, com hem fet en l’exemple de la paella, podem seguir utilitzant el disseny original, que és més fàcil d’entendre.
En aquesta unitat estudiem aquests elements del llenguatge algorísmic:
- Com definir aquests subalgorismes que anomenem funcions i accions.
- Com utilitzar-los des de l’algorisme principal o des d’altres accions i funcions.
- Com pot comunicar-se l’algorisme principal amb les accions o funcions amb què es comunica. En altres paraules, com pot passar i rebre informació (el que anomenem paràmetres).
- En què es diferencien les accions de les funcions.
- Com l’ús d’accions i funcions, a part d’evitar la reescriptura de codi, permet resoldre els problemes d’una manera modular i estructurada.
2. Funcions
Una funció és un conjunt independent d’instruccions que resolen una tasca concreta, que retorna un valor i que pot ser referenciada (invocada o cridada) des d’un altre punt d’un algorisme.
De fet, podem veure una funció com si fos un subalgorisme, amb l’avantatge que es pot cridar (utilitzar) tantes vegades com es vulgui.
2.1. Sintaxi per a la declaració d’una funció
Abans de veure la sintaxi per a la declaració d’una funció, pensem en quins elements seran necessaris per a definir-la:
- Un nom per a poder identificar-la.
- Una sèrie de valors sobre els quals es volen fer els càlculs. Per exemple, en el cas que hem vist del factorial, hauríem d’indicar el número sobre el qual es vol fer el càlcul. Aquests valors reben el nom de paràmetres formals de la funció. Per a cada paràmetre és necessari indicar el seu nom i el seu tipus, com si es declaressin variables. De fet, els paràmetres actuen com a variables dins de la funció.
- Les instruccions pròpiament dites que cal fer a la funció, és a dir, el cos de la funció.
- El valor resultant de la funció, en el nostre exemple, el resultat de calcular el factorial. Cal indicar el tipus de resultat que retorna la funció.
Així doncs, la sintaxi per a declarar una funció és la següent:
[Exemple 14_05]
function name(param1: type1 , param2: type2, ..., paramn: typen): returnType
...
...
return expression;
end function
returnType name(type1 param1, type2 param2, ..., typen paramN) {
...
...
/*returnValue és el valor que calcula la funció*/
return(returnValue);
}
Fixeu-vos que en C, a la declaració dels paràmetres s'utilitza una sintaxi similar a la declaració de variables. Primer es posa el tipus i després el nom del paràmetre.
D'aquesta declaració és molt important el que anomenem la capçalera de la funció. La capçalera és la part que descriu com s'ha de cridar. Indica el nom de la funció, els paràmetres que espera per poder executar-se correctament, i el tipus que en retorna.
Concretament, la capçalera té la següent estructura:
[Exemple 14_06]
function name(param1: type1 , param2: type2, ..., paramn: typen): returntype
returnType name(type1 param1, type2 param2, ..., typen param);
Podem veure que, a excepció del cos de la funció, la capçalera conté tots els elements que hem identificat com a necessaris per a definir-la.
Seguint amb el nostre exemple del factorial, la funció seria:
[Exemple 14_07]
function factorial (number: integer): integer
var
fact: integer;
i: integer;
end var
fact := 1;
i := 1;
while i ≤ number do
fact := fact * i;
i := i + 1;
end while
return(fact);
end function
int factorial(int number) {
int fact;
int i;
fact = 1;
i = 1;
while(i <= number) {
fact = fact*i;
i++;
}
return fact;
}
On hem utilitzat:
- el nom factorial per a identificar la funció;
- un únic paràmetre, en aquest cas un enter, per a identificar el nombre sobre el qual volem fer el càlcul del factorial;
- el tipus de retorn, que també serà enter; i
- el cos de la funció, que fa els càlculs.
Un parell de comentaris sobre les variables i els paràmetres:
- Dins de la funció, solament es poden utilitzar les variables definides dins d’aquesta i els paràmetres formals, que actuen com a variables.
- En una funció, si es modifica el valor d’un paràmetre formal, aquesta modificació no té cap impacte fora de la funció.
2.2. Com utilitzar (cridar) una funció
Una vegada definida la funció, aquesta es pot utilitzar des de l’algorisme principal o des d’una altra funció.
Quan es crida una funció, el control de l’execució de les instruccions passa a la funció. Aquesta executa el codi definit fins a aconseguir la fi de la funció. Llavors el control torna al punt on la funció ha estat cridada.
Per a cridar una funció s’ha de posar el seu nom, seguit d’un parèntesi, la llista de valors que es volen passar com a paràmetres i un parèntesi per a tancar. Els paràmetres utilitzats en la crida reben el nom de paràmetres actuals (o reals). El nombre de paràmetres actuals ha de coincidir en nombre i ordre amb els paràmetres i tipus definits a la capçalera.
Els paràmetres actuals d’una funció poden ser constants, variables o expressions.
A continuació, veiem com es crida una funció a partir de la seva capçalera.
[Exemple 14_08]
{Si suposem que tenim la següent capçalera}
function name(param1: integer , param2: real, param3: char): integer;
{i suposem que tenim la declaració de les següents variables}
var
a:integer;
b:real;
c:char;
result: integer;
end var
{la manera de cridar la funció seria}
result:= name(a, b, c);
Els objectes utilitzats en la crida s’anomenen paràmetres actuals. És a dir, a l'exemple, les variables a, b i c són els paràmetres actuals. A les funcions, els paràmetres actuals poden ser variables, constants o expressions.*/
int name(int param1, float param2, char param3);
// i suposem que tenim la declaració de les variables
int a;
float b;
char c;
int result;
// la manera de cridar la funció seria
result= name(a, b, c);
En el cas del factorial, recordem que la capçalera era:
function factorial (number: integer): integer;
És a dir, té un únic paràmetre formal de tipus enter. Per tant, suposant que n, m i p són tres variables de tipus enter, les possibles maneres de cridar la funció serien
n:= factorial(5); /* utilitzant una constant com a paràmetre actual*/
n:= factorial(p) /* utilitzant una variable com a paràmetre actual */
n:= factorial(m+2) /* utilitzant una expressió com a paràmetre actual */
L’algorisme complet en el cas del factorial seria:
[Exemple 14_09]
function factorial (number: integer): integer
var
fact: integer;
i: integer;
end var
fact := 1;
i := 1;
while i ≤ number do
fact := fact * i;
i := i + 1;
end while
return(fact);
end function
algorithm combinations
var
{definim les variables, dos enters que cal llegir i una on emmagatzemar el resultat}
totalNumColors, colorsToCombine: integer ;
result: integer;
end var
{llegim els 2 nombres}
totalNumColors := readInteger();
colorsToCombine := readInteger();
{Fem el càlcul, perquè ja tenim la manera de calcular el factorial d’un nombre}
result := factorial(totalNumColors) div ( factorial(colorsToCombine) * factorial(totalNumColors - colorsToCombine));
writeInteger(result);
end algorithm
int factorial(int number) {
int fact;
int i;
fact= 1;
i=1;
while( i<=number) {
fact = fact*i;
i++;
}
return fact;
}
int main(int argc, char* argv[]) {
int totalNumColors;
int colorsToCombine;
int result;
scanf("%d", &totalNumColors);
scanf("%d", &colorsToCombine);
result = factorial(totalNumColors) / ( factorial(colorsToCombine) * factorial(totalNumColors -c olorsToCombine));
printf ("%d ", result);
return 0;
}
On hem substituït l’expressió matemàtica m, que no forma part del llenguatge algorísmic, per la crida correcta a la funció que és factorial(m).
3. Accions
Hem vist que una funció és un subalgorisme que rep uns paràmetres i retorna un valor. De fet, una funció té una mecànica de funcionament similar a la d’una funció matemàtica.
Però, de vegades, interessa tan sols disposar d’un subalgorisme que realitzi una sèrie d’instruccions, però que no necessàriament retorni un valor en el sentit matemàtic. Per a aquestes situacions, el llenguatge algorísmic generalitza el concepte de funció i defineix el concepte d’acció.
Una acció és un conjunt independent d’instruccions que resolen una tasca concreta i que pot ser referenciada (invocada o cridada) des d’un altre punt de l’algorisme.
Una acció es diferencia d’una funció perquè:
- No retorna cap valor.
- Quan modifica un paràmetre formal, pot estar també modificant el paràmetre actual, com veurem al següent apartat.
3.1. Sintaxi per a la declaració d’una acció
Igual que una funció, una acció necessita:
- Un nom per a identificar-la.
- Una sèrie de valors sobre els quals es volen fer els càlculs. Aquests valors s’anomenen paràmetres formals de l’acció. Per a cada paràmetre caldrà indicar el seu nom i el seu tipus i, a més, la manera en el qual es comunica aquest paràmetre. Els paràmetres actuen com a variables dins de l’acció.
- Les instruccions que han d’executar-se dins de l’acció, és a dir, el cos de l’acció.
La sintaxi per a definir una acció és igual a la de la funció, excepte per dues coses:
- L’acció no té tipus de retorn, ja que no retorna cap valor.
- En una acció cal indicar davant del nom del paràmetre com es passa. Utilitzem les paraules in, out i inout per a indicar si el paràmetre és d’entrada, sortida o entrada/sortida, és a dir, com es comunica. En la següent secció s’expliquen les diferents maneres de passar els paràmetres a una acció.
[Exemple 14_10]
action name(class1 param1: type1 , class2 param2: type2, ..., classn paramn: typen)
...
...
end action
...
...
}
4. Tipus de paràmetres
A les funcions ja hem vist com es passa un dels tipus de paràmetres tal com es fa a les funcions matemàtiques. És a dir, uns valors que la funció utilitza per a fer els càlculs. Ara bé, com veurem a continuació, hi ha altres maneres de passar els paràmetres i, segons el mètode que s’utilitzi, el comportament serà diferent.
- Paràmetre d’entrada. El valor del paràmetre solament serà consultat i utilitzat dins de l’acció. Aquesta manera de passar paràmetres és típica de funcions matemàtiques i és l’única manera que pot usar-se en les funcions. En els exemples que hem vist fins ara, tots els paràmetres definits han estat d’entrada. Com en l’acció només s’utilitzarà com un valor, una constant, una variable o una expressió, pot ser paràmetre d’entrada.
- Paràmetre de sortida. S’utilitza per a assignar un valor al paràmetre. Si el paràmetre ja té un valor inicial, aquest valor no s’hauria d’utilitzar dins de l’acció. Normalment es passen els paràmetres d’aquesta manera perquè siguin inicialitzats per l’acció. Atès que l’acció deixarà un valor al paràmetre, aquest ha de ser obligatòriament una variable.
- Paràmetres d’entrada/sortida. S’utilitzen per a actualitzar el valor del paràmetre. En aquest cas, el valor inicial del paràmetre es pot utilitzar i també es pot modificar, retornant un nou valor a qui ha cridat l’acció. Atès que l’acció deixarà un nou valor al paràmetre, aquest ha de ser obligatòriament una variable.
Els exemples següents mostren com es modifiquen tant els paràmetres actuals com formals segons la manera en què es passin els paràmetres.
4.1. Exemple 14_11: paràmetres d’entrada
Suposem que disposem d’una acció que, donats el nombre de peces comprades a un majorista i el preu per peça, calcula el cost total i el mostra pel canal estàndard, tenint en compte que segons el nombre de peces s’aplicarà un tipus de descompte o un altre.
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
end const
algorithm example1
var
num:integer;
price: real;
end var
num:= 1005;
price:= 10.0;
computeCost(num, price);
end algorithm
action computeCost(in num: integer, in price: real)
var
val:real;
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= integerToReal(num) * price * (1.0 - discount);
writeReal(val);
end action
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
void computeCost(int num, float price) {
float val;
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
val = (float) (num)*price* (1.0 - discount);
printf("%f", val);
}
int main() {
float price;
int num;
num = 1005;
price = 10.0;
computeCost(num, price);
return 0;
}
L’estat de les variables i paràmetres abans i després d’executar la funció es presenta en el dibuix següent:
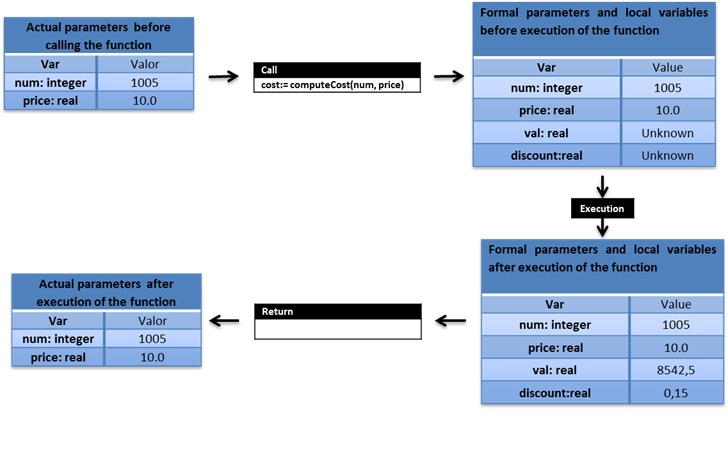
Comentaris:
- Encara que els paràmetres formals i actuals tinguin el mateix nom, es tracta de variables diferents.
- Podem veure que els paràmetres actuals no han canviat.
4.2. Exemple 14_12: paràmetres de sortida
Suposem ara el mateix exemple, però amb una acció que té un paràmetre de sortida per a retornar el cost:
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
end const
algorithm example2
var
num:integer;
price: real;
cost: real;
end var
num:= 1005;
price:= 10.0;
computeCost(num, price, cost);
writeReal(cost);
end algoritm
action computeCost(in num: integer, in price: real, out val: real);
var
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= integerToReal(num) * price * (1.0 - discount);
end action
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
void computeCost(int num, float price, float *val) {
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
*val = (float) (num)*price* (1.0 - discount);
}
int main() {
float price;
int num;
float cost;
num = 1005;
price = 10.0;
computeCost(num, price, &cost);
printf("%f", cost);
return 0;
}
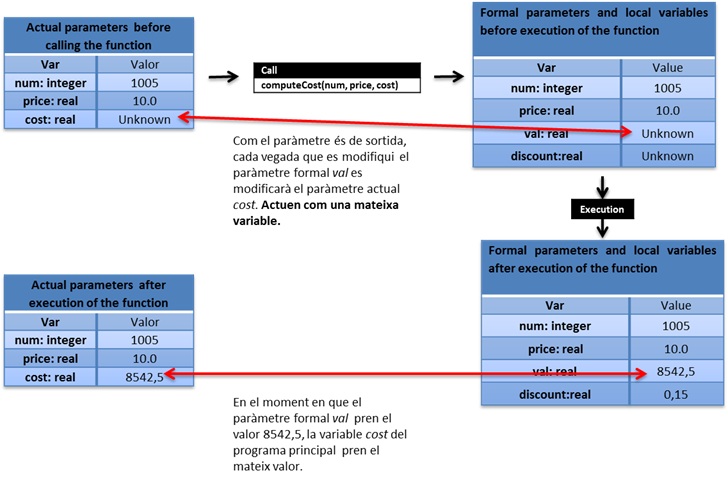
Comentaris:
- En tractar-se d’una acció, es crida sense assignar la tornada a una variable, ja que les accions no retornen cap valor.
- L’acció té un paràmetre formal de sortida. Això vol dir que cada vegada que es modifiqui aquest paràmetre dins de l’acció, automàticament es modificarà amb el mateix valor el paràmetre actual corresponent cost.
- Podem veure que en llenguatge C, els paràmetres de sortida són en realitat punters. Més endavant se’n mostra un exemple.
4.3. Exemple 14_13: paràmetres d’entrada i sortida
Suposem ara que el cost final és la suma d’unes despeses mínimes (cost de lliurament, etc.) més el cost de venda. El cost mínim ve donat per una constant BASIC_COST.
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
BASIC_COST: real = 100.0;
end const
algorithm example3
var
num:integer;
price: real;
cost: real;
end var
num:= 1005;
price:= 10.0;
cost:= BASIC_COST;
computeCost(num, price, cost);
writeReal(cost);
end algoritm
action computeCost(in num: integer, in price: real, inout val: real);
var
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= val + integerToReal(num) * price * (1.0 - discount);
end action
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
#define BASIC_COST 100.0
void computeCost(int num, float price, float *val) {
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
*val = *val + (float) (num)*price* (1.0 - discount);
}
int main() {
float price;
int num;
float cost;
num = 1005;
price = 10.0
cost = BASIC_COST;
computeCost(num, price, &cost);
printf("%f", cost);
return 0;
}
La imatge següent mostra l’estat dels paràmetres i les variables:
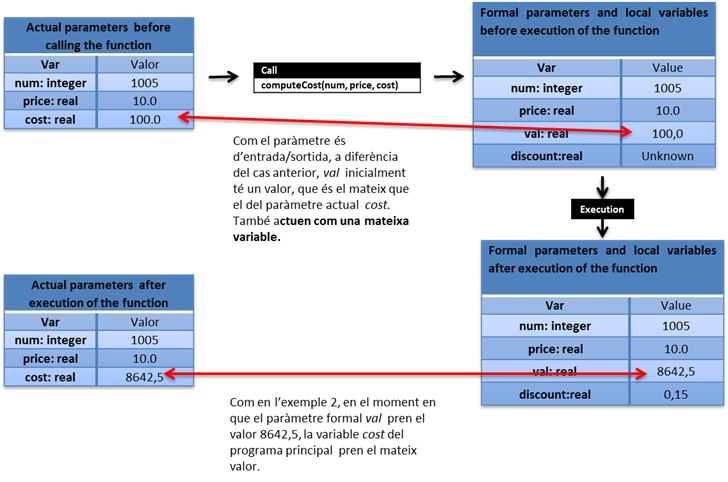
Comentaris:
- L’única diferència amb l’exemple 2 és que el paràmetre val ara és d’entrada i sortida i el seu valor s’actualitza sumant-li el cost de venda.
- D’altra banda, els paràmetres d’entrada i sortida funcionen com els de sortida.
5. Funcions contra accions
Una dels preguntes més freqüents que es plantegen sovint és si davant d’un problema és millor definir una acció o una funció.
Funció: el criteri més important per a decidir que s’ha d’usar una funció és avaluar si aquesta pot actuar com una funció matemàtica que, donats uns paràmetres, pot retornar un valor concret que es pot utilitzar com un membre d’una expressió. Si és així, clarament hem d’escriure una funció.
Acció: si el que ens cal és actualitzar un dels paràmetres o inicialitzar un que no ho està, clarament hem d’utilitzar una acció. També s’utilitza quan no es retorna cap valor o quan s’ha de retornar més d’un.
Moltes vegades les accions tenen alguns paràmetres de sortida, però es podria donar el cas que no tingui cap com, per exemple, en el cas que l’acció llegeixi la informació del canal estàndard i tregui també els resultats directament pel canal estàndard.
6. Accions i funcions predefinides
Tant en el llenguatge algorísmic com en els de programació hi ha algunes accions i funcions ja definides per defecte. Són molt importants perquè faciliten tasques comunes i s’utilitzen amb molta freqüència.
De fet, ja se n’han vist algunes en les unitats anteriors.
Entre d’altres tenim:
- Funcions de conversió de tipus.
- Accions i funcions d’entrada i sortida de dades.
Les funcions de conversió de tipus són aquelles que transformen una variable d’un tipus a un altre. Inclouen:
[Exemple 14_14]
function integerToReal(x: integer):real;
function realToInteger(x: real):integer;
function charToCode(c: char):integer;
function codeToChar(x: integer):char;
int main() {
int x;
float y;
char c;
y = (float) x;
x = (int) y;
x = (int) c;
c = (char) x;
}
Les accions/funcions d’entrada i sortida de dades són aquelles que permeten rebre dades de l’exterior (teclat, fitxers, etc.) i mostrar dades a l’exterior. Inclouen:
[Exemple 14_15]
function readInteger(): integer;
function readReal(): real;
function readChar(): char;
function readString(): string;
action writeInterger(in x: integer);
action writeReal(in x: real);
action writeChar(in x: char);
action writeString(in x: string);
int main() {
int x;
float y;
char c;
string s;
scanf("%d", &x);
scanf("%f", &y);
scanf("%c", &c);
scanf("%s", s);
printf("%d ", x);
printf("%f ", y);
printf("%c ", c);
printf("%s ", s);
return 0;
}
7. Modularització
Hem vist com els llenguatges de programació permeten definir accions i funcions, semblants a subprogrames, que realitzen unes tasques concretes i que poden ser reutilitzades. També hem vist que algunes d’aquestes accions i funcions venen ja predefinides dins del llenguatge, mentre que la majoria seran definides per l’usuari.
Per a mantenir el conjunt d’accions i funcions ordenades i que es puguin utilitzar en diferents programes de manera fàcil, els llenguatges permeten crear llibreries.
Aquestes llibreries consten de dues parts:
- Un fitxer de text que inclou les capçaleres de les accions i funcions que la componen i que en C tenen sempre l’extensió .h.
- El codi de les accions i funcions, que també tindrà una extensió .c, però que solament tindrà el codi de les accions i funcions, sense tenir un main.
Quan s’hagin d’utilitzar des d’algun altre programa solament s’inclouran al programa el fitxer de capçaleres.h. La sintaxi per a incloure-les és:
Concretament, la llibreria que inclou les capçaleres de les accions i funcions d’entrada i sortida de dades s’anomena en C stdio.h. Quan volem utilitzar-la cal incloure al programa:
Hi ha molts exemples de llibreries, per exemple, es podrien crear:
- Llibreries de funcions matemàtiques.
- Llibreries de funcions i accions de tractament de dates.
- Llibreries de funcions de tractament de cadenes de caràcters.
La possibilitat de crear les llibreries facilita la reutilització del codi i estandardització de la manera de treballar.
8. Exercicis d’autoavaluació
- Dissenyeu una funció que donat un enter n calculi els primers n nombres de la sèrie Fibonacci.
2. Dissenyeu una acció que, donats un real que representa el saldo d’un compte corrent i un altre real que representa un càrrec o imposició, actualitzi el saldo del compte.
3. Dissenyeu una funció que calculi n (real) elevat a la potència m (enter).
4. Dissenyeu una acció que, donats tres nombres reals que representen els coeficients d’una equació de segon grau, retorni les seves arrels, en cas que existeixin. En cas contrari, que inicialitzi les arrels a 0.
Recordeu que donada l’equació A * x2 + B * x + C les arrels es calculen:
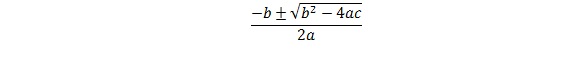
Si l’expressió dins de l’arrel és negativa vol dir que l’equació no té arrels. Podeu suposar que la funció arrel quadrada està ja definida i la seva capçalera és:
function squareRoor(x: real ): real;
4b. Declareu les variables necessàries per a cridar l’acció de l’exercici anterior i indiqueu com es cridaria.
5. Per a cada apartat següent, decidiu si és millor una acció o una funció i definiu la seva capçalera (solament es demana la capçalera, no cal dissenyar cap algorisme).
Donades les dimensions d’una paret (altura i amplària) i el preu de la pintura per metre quadrat, determineu el cost total de pintura necessari per a pintar la paret.
Donat el consum total d’aigua acumulat des del mes de gener fins a juny (tots dos inclosos), llegiu pel canal estàndard el consum de la resta de mesos (des de juliol fins a desembre, tots dos inclosos), i retorneu-lo acumulat al total del consum dels sis primers mesos.
Donats dos nombres enters intercanvieu els valors d’ambdues variables sempre que totes dues siguin diferents de zero.
Donat un enter retorneu la suma dels seus divisors.
5b) Declareu les variables necessàries per a cridar les accions de l’exercici anterior i indiqueu com es cridarien.
9. Solucions
- Dissenyeu una funció que donat un enter n calculi els primers n nombres de la sèrie Fibonacci.
[Exemple 14_16]
function fib( n: integer ): integer;
var
i, value, n+1, n+2: integer;
end var
if n < 3 then
value:= 1;
else
n+1:= 1;
n+2:= 1;
for i:= 3 to n do
value:= n+1 + n+2;
n+2:= n+1;
n+1:= value;
end for
end if
return value;
end function
int fib(int n) {
int i, value, n+1, n+2;
if (n < 3) {
value = 1;
} else {
n+1=1;
n+2=1;
for (i = 3 ; i <= n; i++){
value = n+1 + n+2;
n+2 = n+1;
n+1 = value;
}
}
return value;
}
2. Dissenyeu una acció que, donats un real que representa el saldo d’un compte corrent i un altre real que representa un càrrec o imposició, actualitzi el saldo del compte.
[Exemple 14_17]
action updateBalance(inout balance:real, in amount:real)
balance:=balance + amount;
end action
{només cal actualitzar el saldo (balance) sumant-li la quantitat (amount)}
void updatebalance(float *balance, float amount) {
*balance = *balance + amount;
}
3. Dissenyeu una funció que calculi n (real) elevat a m (enter).
[Exemple 14_18]
function toPower(base: real, power: integer):double
var
total: real;
i: integer;
end var
total:=1;
for i:=1 to power do
total:= total*base;
end for
return total;
end function
double power(float base, int power) {
float total;
int i;
total=1;
for (i=0; i < power; i++) {
total = total * base;
}
return (total);
}
4. Dissenyeu una acció que, donats tres nombres reals que representen els coeficients d’una equació de segon grau, retorni les seves arrels, en cas que existeixin. En cas contrari, que inicialitzi les arrels a 0.
Recordeu que donada l’equació A * x2 + B * x + C les arrels es calculen:
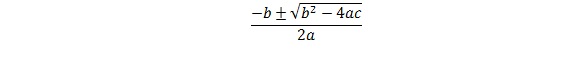
Si l’expressió dins de l’arrel és negativa vol dir que l’equació no té arrels. Podeu suposar que la funció arrel quadrada està ja definida i la seva capçalera és:
ALGORISME: function squareRoor(x: real ): real;
C: double squareRoot(double x);
[Exemple 14_19]
action roots(in a: float, in b:float, in c:float, out root1:float, out root2:float):
var
temp: real;
end var
temp:= b*b -4.0*a*c;
if temp < 0 then
root1:=0;
root2:=0;
else
root1:= (-b+squareRoot(temp))/2.0*a;
root2:= (-b-squareRoot(temp))/2.0*a;
end if
end action
void roots(float a, float b, float c, float *root1, float *root2){
float temp;
temp = b*b -4.0*a*c;
if (temp < 0) {
*root1 = 0;
*root2 = 0;
} else {
root1=(-b+squareRoot(temp)) / (2.0*a);
root2=(-b-squareRoot(temp)) / (2.0*a);
}
}
4b. Declareu les variables necessàries per a cridar l’acció de l’exercici anterior i indiqueu com es cridaria.
[Exemple 14_20]
var
a, b, c: real;
root, root2: real;
end var
{aquí s'inicialitzarien les variables a, b i c}
roots(a, b, c, root1, root2);
int main() {
float a, b, c;
float root1, root2;
/* Aquí s'inicialitzarien les variables a, b i c */
roots(a, b, c, &root1, &root2);
return 0;
}
5. Per a cada apartat següent, decidiu si és millor una acció o una funció i definiu la seva capçalera (solament es demana la capçalera, no cal dissenyar cap algorisme).
5.a.1) Donades les dimensions d’una paret (altura i amplària) i el preu de la pintura per metre quadrat, determineu el cost total de pintura necessari per a pintar la paret.
5.a.2) Donat el consum total d’aigua acumulat des del mes de gener fins a juny (tots dos inclosos), llegiu pel canal estàndard el consum de la resta de mesos (des de juliol fins a desembre, tots dos inclosos), i retorneu-lo acumulat al total del consum dels sis primers mesos.
5.a.3) Donats dos nombres enters intercanvieu els valors d’ambdues variables sempre que totes dues siguin diferents de zero.
5.a.4) Donat un enter retorneu la suma dels seus divisors.
5.a.1) function getCost(height: real, width: real, price_m: real): real
5.a.2) function getTotalConsumption(AcumGenJun: real): real
o
action getTotalConsumption(inout consum: real)
5.a.3) action exchange( inout a: integer, inout b: integer)
5.a.4) function sumDiv (number: integer):integer
float getCost(float height, float width, float price);
/*5.a.2)*/
float getTotalComsumption(float acumGenJun);
/*o*/
void getTotalComsumption(float *acumGenJun);
/*5.a.3)*/
void exchange(int *a, int *b);
/*5.a.4)*/
int sumDiv(int number);
5.b) Declareu les variables necessàries per a cridar les accions de l’exercici anterior i indiqueu com es cridarien.
5.b.2)
action getTotalConsumption(inout acumGenJun: real)
var
consum:float;
end var
{codi d’inicialització ... }
getTotalConsumption(consum);
5.b.3)
action exchange( inout a: integer, inout b: integer)
var
a, b:integer;
end var
/*codi d’inicialització ... */
exchange(a, b);
/*5.b.2)*/
void getTotalComsumption(float *acumGenJun);
float consum;
/*codi d’inicialització ... */
getTotalConsumption(&consum);
/*5.b.3)*/
void exchange(int *a, int *b);
int a, b;
/*codi d’inicialització ... */
exchange(&a, &b);
Resum
En aquesta unitat hem vist com podem estendre els elements elementals del llenguatge algorísmic mitjançant les accions i funcions.
La importància d’aquests elements nous resideix en dos aspectes principals:
- Evitar haver de repetir codi. Davant d’un problema, com hem vist en el càlcul dels nombres combinatoris, on cal repetir diverses línies de codi, definim una funció o acció que contingui aquestes línies de codi que donen solució al problema concret i que, mitjançant el pas de paràmetres, podem executar aquest codi per a diferents valors de les variables, tantes vegades com vulguem.
- Poder dissenyar algorismes complexos d’una manera més simple i estructurada. Ens permet descompondre problemes complexos en subproblemes més senzills i independents entre si. Aquesta tècnica es coneix com a disseny descendent. Aquest aspecte és més important que el primer, ja que és el que ens permet no només resoldre el problema, sinó aconseguir solucions amb funcionalitats independents que siguin més elegants, fàcils d’entendre i de mantenir.
A més, els llenguatges de programació ja inclouen conjunts d’accions i funcions predefinides, com són les de lectura i escriptura de dades i les de conversió de tipus.
També permeten crear llibreries amb accions i funcions definides pels usuaris, que es poden utilitzar sempre que es necessitin per facilitar la reutilització del codi i estandarditzar la manera de treballar.