Iterativa
Objectius
- Entendre el concepte d’estructura iterativa (bucle).
- Tenir clar el «patró» o esquema d’un bucle.
- Comprendre el flux d’execució d’un programa amb estructures iteratives.
- Saber reflexionar sobre la condició de final d’un bucle.
- Aprendre a construir una estructura de control iterativa.
- Conèixer les diferents variants de l’estructura iterativa: while i for.
- Saber resoldre problemes senzills utilitzant estructures iteratives.
- Saber resoldre problemes senzills combinant els tres tipus d’estructures: seqüencial, alternativa i iterativa.
- Aplicar l’estructura iterativa al recorregut d’una seqüència.
Introducció
En aquesta unitat es presenten les estructures de control de flux iteratives que s’afegeixen a les estructures de control seqüencial i alternativa que ja coneixem per a controlar dinàmicament l’execució d’un programa. És el que es coneix també com a bucle o loop. Veurem que amb aquesta estructura, un programa pot executar repetidament un bloc d’instruccions sempre que es compleixi una determinada condició.
1. Estructura (o composició) iterativa: aproximació intuïtiva
Amb les estructures que ja coneixem podem resoldre diversos problemes, però no uns altres, per als quals necessitem l’estructura iterativa. L’estructura iterativa està molt present en la vida quotidiana. Fixeu-vos en la següent instrucció d’una recepta de cuina: Mentre la salsa no estigui prou lligada, remeneu a foc lent. O en aquest altre pensament: Vaig amb bici mentre tingui ganes. Es tracta, doncs, de repetir una mateixa acció mentre es compleixi una determinada condició. No debades, el verb iterar és sinònim del verb repetir.
En el diagrama de flux següent es presenten les parts d’una estructura iterativa. Les fletxes indiquen el sentit del flux d’execució.
En primer lloc es fa la consulta sobre l’estat actual o condició (rombe verd) i segons el valor resultat de l’avaluació (cert o fals) hi ha dos possibles camins que cal seguir: si l’avaluació dona cert s’executa el bloc d’instruccions (rectangle groc) i es torna a avaluar la condició. Si no, si el resultat és fals, el flux d’execució continua tenint un sol camí (rombe blau de finalització ) i s’acaba la iteració.
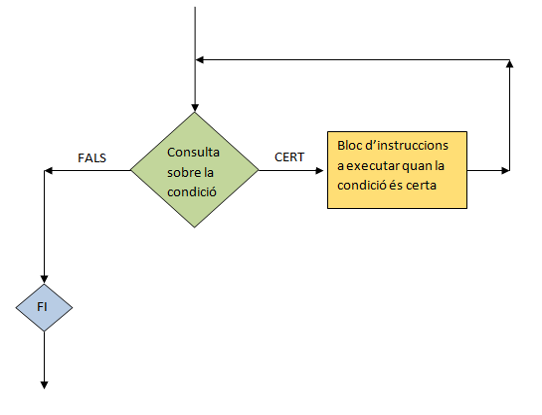
El primer pas és consultar l’estat actual o condició. Aquí s’avalua una expressió lògica que dona com resultat un valor booleà (cert o fals). Segons el resultat, o bé s’executaran les instruccions del bucle (quan el resultat és cert) i es tornarà al punt d’avaluació de la condició, o bé, quan el resultat és fals, es continuarà amb l’execució de la resta del programa i s’acabarà la iteració.
Vegem a continuació alguns exemples d’ús de l’estructura iterativa. Per a il·lustrar com funciona el flux d’execució es presenta un diagrama per a cada exemple.
1.1. Exemple 10_01 - Recepta de cuina
Per a la recepta de cuina anterior Mentre la salsa no estigui prou lligada, remeneu a foc lent, si identifiquem les parts de l’estructura alternativa obtenim el següent diagrama de flux d’execució:
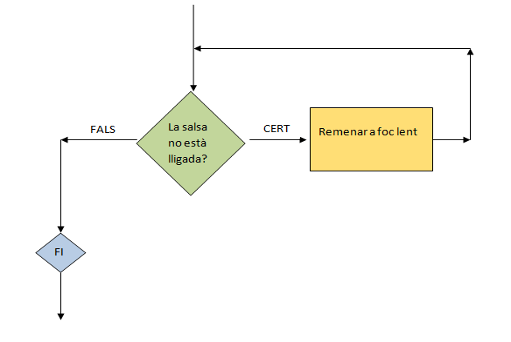
Per tant, estarem remenant la salsa a foc lent mentre no estigui lligada. Fixeu-vos que en aquest exemple la condició del mentre està formulada en negatiu Mentre no estigui lligada...
1.2. Exemple 10_02 - Anar amb bici
Si representem el pensament anterior Vaig amb bici mentre tingui ganes, obtenim el següent diagrama de flux:
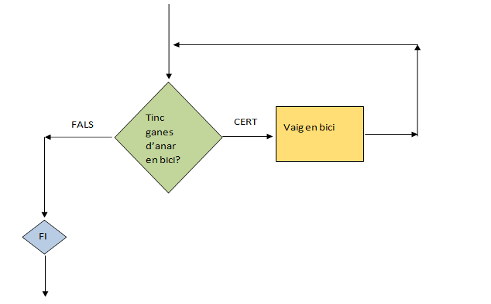
1.3. Exemple 10_03 - Paret
Pensem ara en el cas d’un paleta que va pujant una paret de maons. Ha d’anar afegint files de maons fins que la paret arribi al sostre. El procés segueix el següent diagrama de flux:
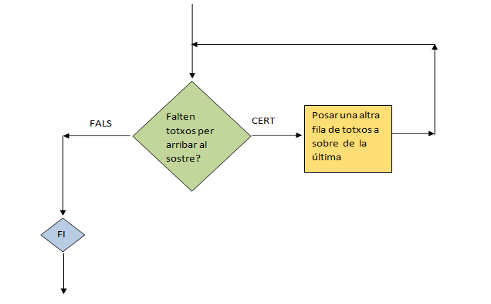
2. Codificació d’una estructura iterativa
En aquest apartat presentem la codificació d’una estructura de control iterativa, en aquest cas l’estructura while, que és la més general. Veurem després que admet altres variants.
| Parts | Codificació en llenguatge algorísmic |
|---|---|
| Consulta sobre l’estat actual o condició | while expressió condicional do |
| Què fer quan la condició és Certa | bloc d’instruccions |
| Marca de finalització d’estructura iterativa | end while |
2.1. Exemple 10_04 - Paret
A continuació teniu codificat un primer algorisme tant en llenguatge algorísmic com en C. Imaginem que tenim un robot automàtic capaç de construir parets. Suposarem implementada l’acció buildWall(), que s’encarrega de fer l’operació necessària per a afegir una fila de maons damunt de la paret respectivament.
algorithm ferParet
var
alçadaParet: real;
alçadaSostre: real;
end var
llegirAlçadaParet(alçadaParet);
llegirAlçadaSostre(alçadaSostre);
while alçadaParet < alçadaSostre do
pujarParet();
llegirAlçadaParet(alçadaParet);
end while
end algorithm
float alsadaParet, alsadaSostre;
scanf("%f", &alsadaParet);
scanf("%f", &alsadaSostre);
while ( alsadaParet < alsadaSostre ) {
pujarParet();
scanf("%f", &alsadaParet);
}
return 0;
}
Analitzem l’execució de l’estructura iterativa:
| # Línia | Codi |
|---|---|
| 1 | while hightWall < hightCealing do |
| 2 | bildWall(); |
| 3 | hightWall:= readReal(); |
| 4 | end while |
La línia 1 avalua la condició:
Cas cert: si l’altura de la paret és inferior a la del sostre, llavors l’expressió és certa i s’executarà la línia 2 de codi. És a dir, el robot pujarà la paret afegint una fila de maons nova. Una vegada executada l’acció de la línia 2, el control del programa passa a la línia 3 del codi i s’obté la nova altura, després de la qual torna de nou a la línia 1 (bucle). Fixeu-vos que la funció buildWall() està modificant l’altura de la paret i, per tant, quan tornem a executar la línia 1, l’altura de la paret ja serà diferent.
Caso fals: en cas que la condició no sigui certa (per tant, la paret ja toca el sostre), el resultat de l’expressió és fals i no s’executarà la línia 2, sinó que passarem directament a la línia 4.
2.2. Exemple 10_05 - Multiplicació
A continuació teniu codificat un algorisme tant en llenguatge algorísmic com en llenguatge C per a multiplicar dos nombres enters qualssevol (n*m) sense utilitzar l’operador de multiplicació *. Aquest és un exemple clàssic per a entendre l’ús de l’estructura iterativa. Si no disposem de l’operador * podem fer igualment la multiplicació de dos enters a partir de la suma. Per això caldrà sumar m vegades un nombre n. Ex. 2*5= 2+2+2+2+2, sumar cinc vegades el número 2.
algorithm multiplicacioEnters
var
n: integer;
m: integer;
x: integer;
end var
n:= readInteger();
m:= readInteger();
x:=0;
while m ≠ 0 do
x:=x+n;
m:=m-1;
end while
writeInteger(x);
end algorithm
int main(int argc, char** argv) {
int n, m, x;
scanf("%d", &n);
scanf("%d", &m);
x = 0;
while ( m != 0 ) {
x = x + n; // Equivalence in C language: x += n;
m = m - 1; // Equivalence in C language: m--;
}
printf("%d", x);
return 0;
}
En aquest exemple, ens cal una variable auxiliar x on anirem guardant els resultats parcials. Haurem d’inicialitzar-la a 0.
2.3. Exemple 10_06 - Factorial
En aquest cas, dissenyarem un algorisme per a resoldre un problema matemàtic, el càlcul del factorial d’un nombre enter positiu. El factorial d’un nombre es calcula així:
factorial(0) = 1 i
factorial(n) = n * factorial(n-1).
Per a fer el càlcul cal multiplicar tots els nombres entre 1 i el nombre del qual volem calcular el factorial.
algorithm factorial
var
n: integer;
i: integer;
fact: integer;
end var
n:= readInteger();
i:= 1:
fact:= 1;
while i ≤ n do
fact:= fact*i;
i:= i+1;
end while
writeInteger(fact);
end algorithm
int main(int argc, char** argv) {
int n, i, fact;
scanf("%d", &n);
i = 1;
fact = 1;
while ( i <= n ) {
fact = fact * i;
i = i + 1;
}
printf("%d", fact);
return 0;
}
| # Línia | Codi |
|---|---|
| 1 | while i<=n do |
| 2 | fact:=fact*i; |
| 3 | i:=i+1; |
| 4 | end while |
Analitzant l’execució de l’estructura iterativa, observeu que cada vegada que s’executa la línia 1 el valor de la variable i és diferent. Si ni els valors d’i ni els de n es modifiquessin dins del bucle, no podríem sortir mai de la composició.
2.4. La condició de final del bucle
Un aspecte sobre el qual cal posar molta atenció quan utilitzem estructures iteratives és assegurar-nos que el bucle acabarà en algun moment. Si no ho fem bé, podria passar que el bucle fos infinit i l’algorisme no acabés mai. Per tant, assegurem-nos sempre que això no passarà. Hi ha mètodes formals per a assegurar que la construcció està ben definida i que el bucle sempre acaba, però no els estudiarem encara. De tota manera, intuïtivament també podem deduir que el bucle acabarà en algun moment. Vegem-ho en alguns dels exemples que hem treballat anteriorment.
Recordem l’algorisme per a calcular el factorial d’un nombre enter positiu.
algorithm factorial
var
n: integer;
i: integer;
fact: integer;
end var
n:= readInteger();
i:=1;
fact:=1;
while i ≤ n do
fact:= fact*i;
i:= i+1;
end while
writeInteger(fact);
end algorithm
int main(int argc, char** argv) {
int n, i, fact;
scanf("%d", &n);
i = 1;
fact = 1;
while ( i <= n ) {
fact = fact * i;
i = i + 1;
}
printf("%d", fact);
return 0;
}
| # Línia | Codi |
|---|---|
| 1 | i:=1: |
| 2 | fact:=1; |
| 3 | while i<=n do |
| 4 | fact:=fact*i; |
| 5 | i:=i+1; |
| 6 | end while |
Observant l’execució de l’algorisme veiem que:
- Les instruccions de dins del bucle (línies 4 i 5) s’executaran almenys una vegada, tret que el nombre al qual s’hagi de calcular el factorial sigui 0.
- En cada iteració, és a dir, cada vegada que entrem dins del cos del bucle (línies 4 i 5), la variable i s’incrementa en una unitat. Por tant, cada vegada que s’executa la línia 3, on s’avalua la condició, el valor de la variable i és diferent. Concretament, val una unitat més. D’aquesta manera, va augmentant el seu valor des d’1 fins a arribar al valor n. Per tant, el bucle acabarà en algun moment, quan l’expressió (i<=n) deixi de ser certa. Això és, quan la variable i contingui un valor superior al nombre n.
Però, què passaria si haguéssim oblidat incrementar el valor de la variable i dins del cos del bucle?
| # Línia | Codi |
|---|---|
| 1 | i:=1: |
| 2 | fact:=1; |
| 3 | while i<=n do |
| 4 | fact:=fact*i; |
| 5 | end while |
La variable i sempre valdria 1, així que el bucle seria infinit, no acabaria mai tret que el valor de la variable n fos també 1. És a dir, que l’algorisme solament funcionaria en el cas del càlcul del factorial del número 0. Per a la resta de nombres positius no funcionaria. El programa es quedaria bloquejat en un bucle sense fi. Diguem que es «penjaria» perquè no hem controlat bé la fi del bucle i ens veuríem immersos en infinites iteracions.
Assegureu-vos sempre, doncs, que en cada iteració (volta) del bucle quedin menys iteracions per fer.
3. Variant de l’estructura iterativa
3.1. La construcció while
La construcció while que acabem de veure permet expressar qualsevol composició d’instruccions que calgui repetir d’acord amb unes condicions determinades. És, doncs, la construcció iterativa més general. Alguns llenguatges, no obstant això, inclouen altres construccions iteratives que són variants d’aquesta i que només es poden aplicar en casos molt concrets, sempre que es donin determinades circumstàncies. En aquest apartat veurem també la construcció for.
Recordeu que l’estructura del while és la següent:
| Parts | Codificació en llenguatge algorísmic |
|---|---|
| Consulta sobre l’estat actual o condició | while expressió condicional do |
| Què fer quan la condició és certa | bloc d’instruccions |
| Marca de finalització d’estructura iterativa | end while |
3.2. La construcció for
La variant for s’utilitza quan cal repetir un bloc d’instruccions un nombre conegut de vegades. Per exemple, en el cas del factorial que hem vist anteriorment, sabem que hem de repetir un mateix càlcul (fact * i) un nombre determinat de vegades, en aquest cas des d’1 fins al nombre del qual volem calcular el factorial. Si utilitzem la instrucció for l’estructura iterativa se simplifica.
[Exemple 10_07]
algorithm factorial2
var
n: integer;
i: integer;
fact: integer;
end var
n := readInteger();
fact:=1;
for i:=1 to n do
fact:= fact*i;
end for
writeInteger(fact);
end algorithm
int main(int argc, char** argv) {
int n, i, fact;
scanf("%d", &n);
fact = 1;
for ( i = 1; i <= n; i++ ) {
fact = fact * i;
}
printf("%d", fact);
return 0;
}
| # Línia | Codi |
|---|---|
| 1 | for i:=1 to n do |
| 2 | fact:=fact*i; |
| 4 | end for |
Si us hi fixeu, en el cas de l’estructura iterativa for, les línies de codi que hi ha dins del bucle són menys. En aquest cas, només una, la línia 2. Això és així perquè l’estructura for ja s’encarrega d’anar incrementant el valor de l’índex de la primera línia (en aquest cas la i des del valor inicial, que s’indica en la mateixa estructura for (1) fins al valor final (n), que també s’indica en la mateixa línia. Observeu també que en aquest cas no cal iniciar abans de l’estructura iterativa la variable i. Per tant, ens hem estalviat dues línies de codi en relació amb la resolució del mateix problema amb l’estructura while.
L’esquema de l’estructura de control for és, doncs, la següent:
| Parts | Codificació en llenguatge algorísmic |
|---|---|
| Inicialització de la variable de control i indicació del nombre de vegades que cal repetir la iteració | for índex:= valor inicial to valor final do |
| Què fer | bloc d’instruccions |
| Marca de finalització de l’estructura iterativa | end for |
Tingueu en compte que, en aquest cas, l’estructura for ja s’encarrega d’anar incrementant el valor de l’índex en cada iteració.
El C té una sintaxi de la composició iterativa for idèntica. Dins del parèntesi tenim tres parts separades per ‘ ;’ (punt i coma). Cadascuna de les parts exerceix un paper en la composició.
/* loop body */
}
- expression1: és la part d’inicialització. En aquest primer segment assignem el valor inicial a la variable comptador (i = 1).
- expression2: conté el test de continuïtat. Si l’avaluació de l’expressió 2 és certa es passarà a executar el cos del bucle. Si resulta falsa es continuarà l’execució amb la instrucció immediatament posterior al cos de la composició.
- expression3: és la part d’actualització del comptador. L’expression3 s’avaluarà quan s’acabi d’executar el cos del bucle i abans de passar a avaluar el test. En aquesta part es troba la instrucció que modifica la variable comptador (i++).
Així doncs, sempre que coneguem el nombre d’iteracions que caldrà fer, serà més còmode utilitzar la construcció for en lloc de la construcció while, ja que ens estalviem haver d’inicialitzar la variable índex i també haver d’anar incrementant cada iteració. Però recordeu que no totes les iteracions es poden representar amb una estructura for!
3.2.1. Modificadors de la composició
La forma que hem vist de la composició iterativa for (que en cada volta s’incrementa el comptador en una unitat) és la més habitual. Però no respon a tots els plantejaments amb els quals ens podem trobar.
- Volem simular un compte enrere des d’un valor determinat fins a 0.
- Volem fer la suma de tots els nombres parells entre dos nombres entrats.
És clar que tots dos problemes els resoldríem amb algun tipus de composició iterativa, però, malgrat saber la quantitat de voltes que cal realitzar, la composició for original no ens és útil per a diferents problemes.
- Si fem un compte enrere, ens interessaria anar baixant el valor del comptador i no pujar-lo.
- Si volem sumar parells, aniria bé poder incrementar el comptador de dues en dues unitats.
La composició for disposa de variants que faciliten la feina.
3.3. Exemples
3.3.1. Exemple 10_08 – Compte enrere
algorithm countDown
var
n: integer;
k: integer;
end var
n := readInteger();
for k:=n to 0 do step -1
writeInteger(k);
end for
end algorithm
int main(int argc, char** argv) {
int n, k;
scanf("%d", &n);
for ( k = n; k > 0; k-- ) {
printf("%d", k);
}
return 0;
}
3.3.2. Exemple 10_09 - Sumador de parells
Volem sumar els nombres parells compresos entre dos nombres n i m que compleixen que n <= m.
algorithm evenAdd
var
n:integer;
m:integer;
k:integer;
sum:integer;
end var
n := readInteger();
m := readInteger();
if (n mod 2 ≠ 0)
n := n + 1;
end if
sum:= 0;
for k:=n to m do step 2
suma := sum + k;
end for
writeInteger(sum);
end algorithm
int main(int argc, char** argv) {
int n, m, k, sum;
scanf("%d %d", &n, &m);
sum = 0;
if (n % 2 > 0)
n++;
for ( k = n; k <= m; k += 2 ) {
sum = sum + k;
}
printf ("%d", sum);
return 0;
}
3.3.3. Exemple 10_10 – Temperatura mitjana
En la unitat anterior hem vist l’estructura de dades tipus vector. Utilitzant aquesta estructura, escrivim l’algorisme per a calcular la temperatura mitjana d’una setmana:
algorithm meanTemp
var
t: vector[7] of real;
m: real;
end var
t[1] := readReal();
t[2] := readReal();
t[3] := readReal();
t[4] := readReal();
t[5] := readReal();
t[6] := readReal();
t[7] := readReal();
m:=(t[1] + t[2] + t[3] + t[4] + t[5] + t[6] + t[7]) /7;
writeReal(m);
end algorithm
Ara que coneixem l'estructura iterativa while i aprofitant que l'algorisme repeteix un conjunt d'instruccions el podem simplificar de la següent manera:
algorithm meanTemp
var
t: vector[7] of real;
m: real;
i: integer;
end var
i := 1;
m := 0;
while i ≤ 7 do
t[i] := readReal();
m := m +t [i];
i := i + 1:
end while
writeReal(m/7);
end algorithm
int main(int argc, char** argv) {
float t[7];
float m;
int i;
i = 0; // the base index of array is 0 in C language
m = 0;
while ( i < 7 ) { // "<=" is changed by "<" because in C language last element of a N-size array is N-1
scanf("%f", &t[i]);
m = m + t[i];
i = i + 1;
}
printf("%f", m / 7);
return 0;
}
D’aquesta manera, la instrucció per a llegir la temperatura només cal escriure-la una vegada. Però, què passaria si ara volguéssim calcular la temperatura de tot l’any? S’hauria de definir un vector amb capacitat per a 365 elements i. L’algorisme pràcticament seria el mateix:
[Exemple 10_11]
algorithm meanTemp
var
t: vector[365] of real;
m: real;
i: integer;
end var
i:=1;
m:=0;
while i ≤ 365 do
t[i] := readReal();
m:= m+t[i];
i:= i+1:
end while
writeReal(m/365);
end algorithm
int main(int argc, char** argv) {
float t[365];
float m;
int i;
i = 0;
m = 0;
while ( i < 365 ) {
scanf("%f", &t[i]);
m = m + t[i];
i = i + 1;
}
printf("%f", m / 365);
return 0;
}
Una millor opció seria utilitzar l’estructura for, aprofitant que sabem quants elements del vector és necessari recórrer. A més, declarant la constant days es pot adaptar el programa amb més facilitat. Vegem-ho:
[Exemple 10_12]
algorithm meanTemp
const
DAYS: integer = 365;
end const
var
t: vector[DAYS] of real;
m: real;
end var
m:=0;
for i:=1 to DAYS do
t[i] := readReal();
m := m + t[i];
end for
writeReal(m / DAYS);
end algorithm
#define DAYS 365
int main(int argc, char** argv) {
float t[DAYS];
float m;
int i;
m = 0;
for ( i = 0; i < DAYS; i++ ) {
scanf("%f", &t[i]);
m = m + t[i];
}
printf("%f", m / DAYS);
return 0;
}
Vegem, doncs, que l’estructura for és molt útil per a recórrer els elements d’un vector. Reprendrem aquest concepte de recorregut més endavant, en una unitat posterior, quan parlem dels esquemes algorísmics de recorregut i de cerca.
3.3.4. Exemple 10_13 – Ha gelat
Per a acabar, imaginem ara la situació següent. Disposem d’un registre de les temperatures de tot l’any, que tenim emmagatzemades en un vector, de la mateixa manera que hem fet a l’exemple anterior. Ara volem descobrir si algun dia ha gelat. Això equival a anar comprovant si alguna de les temperatures és negativa.
algorithm hasFrozen?
var
t: vector[365] of real;
frozen: boolean;
i: integer;
end var
i:=1;
frozen:= false;
while i ≤ 365 and frozen = false do
t[i] := readReal();
if t[i] ≤ 0 then
frozen:= true;
end if
i:= i+1:
end while
writeBoolean(frozen);
end algorithm
typedef enum {FALSE, TRUE} boolean;
int main(int argc, char** argv) {
float t[365];
boolean frozen;
int i;
i = 0;
frozen = FALSE;
while ( i < 365 && frozen == FALSE ) {
scanf("%f", &t[i]);
if ( t[i] < 0 )
frozen = TRUE;
i = i + 1;
}
printf("%d", frozen); // Equivalence in C language: 0 == FALSE, 1 == TRUE
return 0;
}
Fixeu-vos que quan trobem el primer cas de temperatura negativa, ja podem acabar; no cal que seguim revisant més temperatures. Solament volem saber si algun dia ha gelat, no quants o quins dies ha gelat.
Si volguéssim saber quants dies ha gelat, llavors hauríem de revisar tots els elements del vector i en aquest cas seria més adequada una estructura for. Vegem-ho:
3.3.5. Exemple 10_14 – Compte de dies
algorithm howManyDaysHasFrozen?
var
t: vector[365] of real;
numDays: integer;
end var
numDays:= 0;
for i:= 1 to 365 do
t[i]:= readReal();
if t[i] ≤ 0 then
numDays:= numDays+1;
end if
end for
writeInteger(numDays);
end algorithm
int main(int argc, char** argv) {
float t[365];
int i, numDays;
numDays = 0;
for ( i = 0; i < 365; i++ ) {
scanf("%f", &t[i]);
if ( t[i] < 0 )
numDays = numDays + 1;
}
printf("%d", numDays);
return 0;
}
Observeu que en aquest exemple hem utilitzat l’estructura iterativa for i, dins del cos, l’estructura alternativa.
Una vegada presentada l’estructura de control iterativa, coneixem ja totes les estructures de control de flux de l’execució d’un codi: seqüencial (una instrucció a continuació d’una altra), alternativa i iterativa. Per tant, a partir d’ara, utilitzant combinacions d’aquestes tres estructures de control podem resoldre qualsevol problema.
Resum
En aquesta unitat hem definit l’estructura iterativa amb les seves variants principals. Aquest tipus d’estructura és fonamental per a controlar el flux d’execució d’un programa i completa les estructures de control de flux necessàries per a resoldre qualsevol problema i que són tres: seqüencial, alternativa i iterativa.
Hem utilitzat el grafisme dels diagrames de flux per a mostrar el funcionament d’aquesta estructura de control i hem donat èmfasi a la importància d’assegurar la condició de final del bucle per a garantir que el programa funcionarà bé.
Hem vist diversos exemples d’estructura alternativa juntament amb la seva traducció al llenguatge algorísmic i al llenguatge C considerant diverses possibilitats variants, des de la construcció while, d’ús general, fins a la construcció for, que es pot utilitzar en els casos en què coneguem d’entrada el nombre d’iteracions que cal fer.
Finalment hem vist alguns exemples d’ús combinat de les tres estructures de control de flux (seqüencial, alternativa i iterativa) i de tipus de dades estructurades, com és el cas dels vectors.