Con este Manual de visualización de datos vamos a aprender a generar los principales tipos de gráfico, ya que los gráficos de una, dos y más dimensiones son una parte fundamental de la programación estadística. Cuando trabajamos con datos es indispensable saber transformar la información en gráficos, no sólo para poder transmitirla a terceras personas de una manera visual, rápida y clara, sino también para nosotros mismos, ya que una buena visualización nos ayudará muchas veces a descubrir aspectos de nuestros datos que desconocíamos.

            Este manual es de tipo práctico y veremos ejemplos que se pueden trabajar desde cualquier ordenador que tenga R instalado ya que usaremos datos que vienen por defecto con la instalación estándar de R. El énfasis lo hemos querido poner en usar el menor número posible de comandos para sacar las visualizaciones más útiles y potentes. Asimismo, hablamos de la importancia de entender la naturaleza de los datos para elegir un tipo u otro de gráfico de forma óptima. Luego, la audiencia también es muy importante a la hora de elegir el tipo de gráfico: un histograma lo entiende casi todo el mundo a simple vista, mientras que un box plot a veces requiere de alguna explicación adicional. También deben tener en cuenta que el sistema visual de los humanos es particularmente bueno a la hora de interpretar longitudes y posiciones de forma cuantitativa , pero no tanto a la hora de interpretar líneas sueltas y ángulos, o áreas y volúmenes. Por esta razón los histogramas, los box plots y los gráficos de dispersión y de puntos suelen ser buenas opciones, mientras que los gráficos de sectores (pie charts) no son recomendados y no deberían usarse nunca excepto para intentar dar una percepción irreal de los datos! Finalmente, la mayoría de las personas distinguimos los colores sin dificultad, pero hasta un 10% de los hombres (y un porcentaje mucho menor en mujeres) son daltónicos y no distinguen combinaciones específicas de colores (https://es.wikipedia.org/wiki/Daltonismo). La combinación de colores que deberían evitar siempre es el rojo y el verde. Los colores sirven para hacer diferencias cualitativas en una visualización, pero no deben usarse para intentar transmitir valores cuantitativos ya que nuestro sistema visual no está lo suficientemente desarrollado para ello.

Finalmente, recomendamos el uso de R Studio, un IDE (“Integrated Development Environment”) increíblemente útil donde a la vez de introducir tu código puedes ver lo que estás haciendo en cuanto se refiere al propio código, objetos en uso, gráficos que vas generando e incluso las páginas de ayuda que vas consultando sobre las diferentes funciones.

Nota general: una cosa muy importante es siempre tener en cuenta si los datos que queremos representar son de un único tipo de valor (es decir, una única variable, como la altura, el peso, etc, aunque esté dividida por edades, genero, etc), o de dos o más tipos de valor (por ejemplo, el precio de un billete de avión y lo lejos que te lleva). Para representar dos o más variables se usan scatter plots (seccion 6), y para representar un único tipo de valor, todos los demás tipos de gráfico (secciones 2-5).

1. Gráficos de "tallo y hojas" y "de puntos" (stem-and-leaf y dot plots)
   1. Gráficos de "tallo y hojas" (stem-and-leaf)
   2. Gráficos de puntos (dot plots)
2. Gráficos de barras (bar charts)
3. Histogramas y gráficos de densidad kernel (kernel density plots)
   1. Histogramas
   2. Diagramas de densidad kernel (kernel density plots)
4. Box plots (diagramas de caja)
   1. Comparación de box plots por especie
   2. Diagramas de violín
5. Gráficos de dispersión (scatter plots)
   1. Ejemplos con mtcars

Gráficos de "tallo y hojas" y "de puntos" (stem-and-leaf y dot plots)

Los gráficos de “tallo y hojas” (stem-and-leaf) y “de puntos” (dot plots) son de los gráficos más sencillos que existen, pero a la vez son muy útiles porque te permiten tener una visión rápida de la distribución de los datos. También los gráficos “stem-and-leaf” y “dot plots” sirven para ilustrar las enormes capacidades de R como herramienta de visualización de datos.

Los datos que vamos a utilizar son un dataset que se llama mtcars, un data frame que viene cargado por defecto con la distribución de R. Se trata simplemente de un grupo de coches y sus características técnicas, y pueden acceder a mtcars desde una interfaz a R de esta manera:

mtcars es un data frame de 32 filas x 11 columnas. Con la función head() sólo nos saca las 6 primeras filas.

Gráficos de "tallo y hojas" (stem-and-leaf)

FUNCION PRINCIPAL: stem()

Los gráficos de tallo y hojas (stem-and- leaf) se usan para mostrar frecuencias de valores. Puedes hacer una distribución de frecuencia usando tanto un histograma como un gráfico de tallo y hojas; la diferencia es que con un histograma, aunque te muestra la frecuencia que hay para cada clase de valores, pierdes los números originales. Con un gráfico de stem and leaf sigues reteniendo los valores originales y también te informa de la frecuencia de los mismos. Asi, un grafico de tallo y hojas te da la misma información que un histograma y además no pierdes los valores originales.

Ya que el punto decimal viene dado por la barra vertical (|), la primera fila (10 | 44) se interpreta como que existen dos valores que son 10.4 y 10.4. La sexta fila (10 | 02258) se traduce en los valores 15.0, 15.2, 15.2, 15.5 y 15.8.

Pueden probar a cambiar la opción scale, que cambia el número de compartimientos. Por ejemplo:

Gráficos de puntos (dot plots)

FUNCION PRINCIPAL: dotchart()

Ahora vamos a representar los mismos datos, las ‘Millas por galón’ agrupados en función del número de cilindros de un coche usando un gráfico de puntos, que nos permitirá ver la relación que existe entre el número de cilindros de los diferentes modelos de coche y las millas que pueden cubrir por cada galón de gasolina.

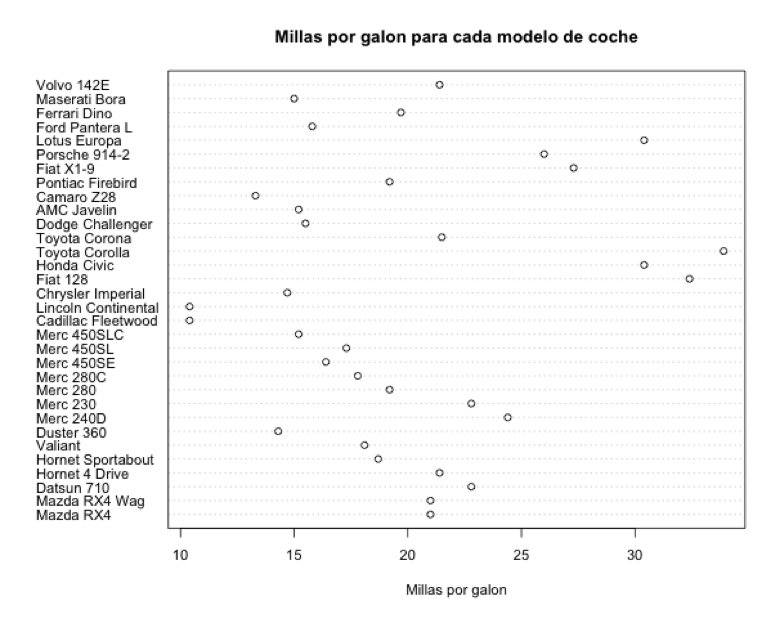
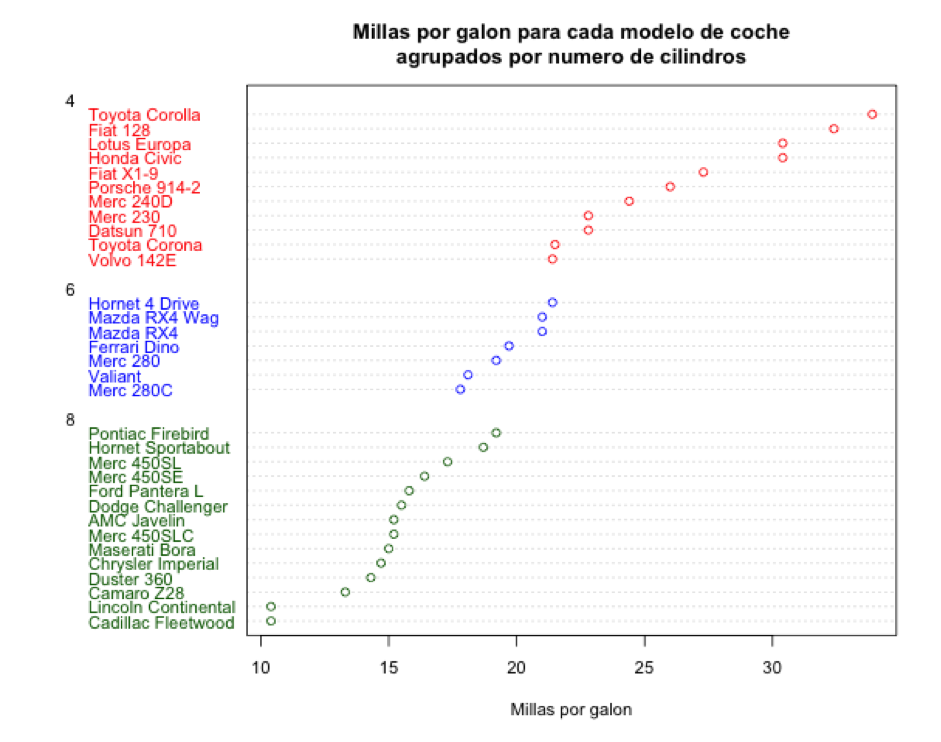
Ahora mostramos las Millas por galón de cada coche y coloreamos por número de cilindros. El atributo group te especifica cómo agrupamos los valores con los que estamos generando el gráfico.

Gráficos de barras (bar charts)

FUNCION PRNCIPAL: barplot()

Un gráfico de barras se usa para representar valores de un único tipo. El dataset que vamos a usar se llama VADeaths, viene por defecto con la distribución estándar de R, y es una estadística de la mortalidad en el estado norteamericano de Virginia en el año 1940.

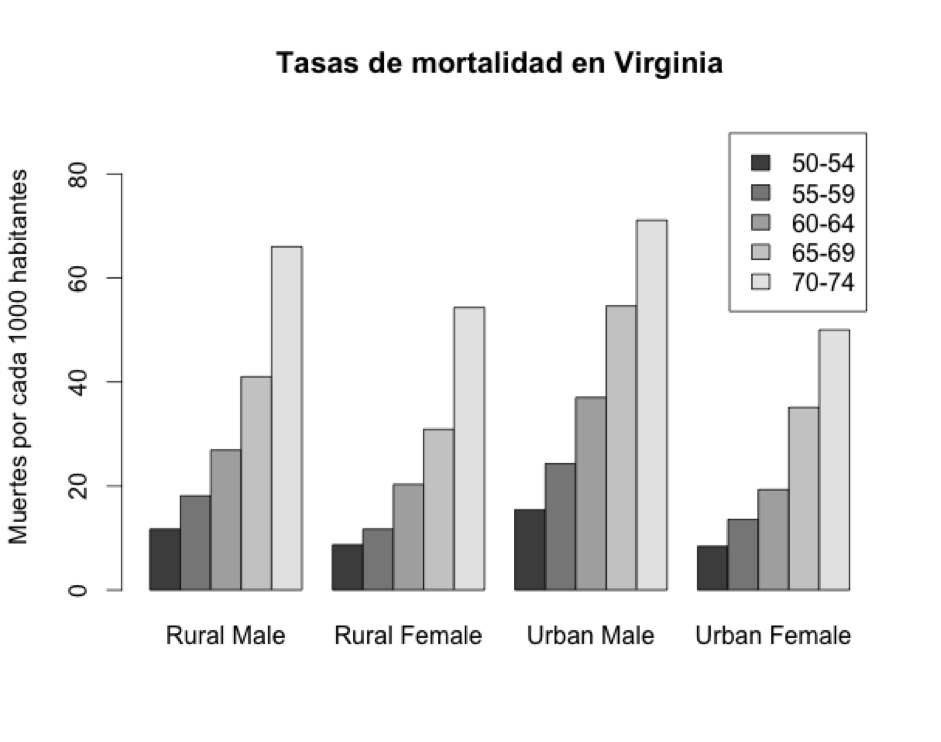
·legend=TRUE: especifica que dibuje una leyenda con los valores para ayudarte a interpretar las barras

·ylim=c(0,90): especifica que la escala vaya de 0-90

·ylab: leyenda del eje Y

·main: título del gráfico

Vamos cambiando algunas opciones de la función barplot() para ver para qué sirven:

·beside=FALSE: te pone los valores apilados en vez de las barras separadas, lo cual es mucho peor para distinguir los valores

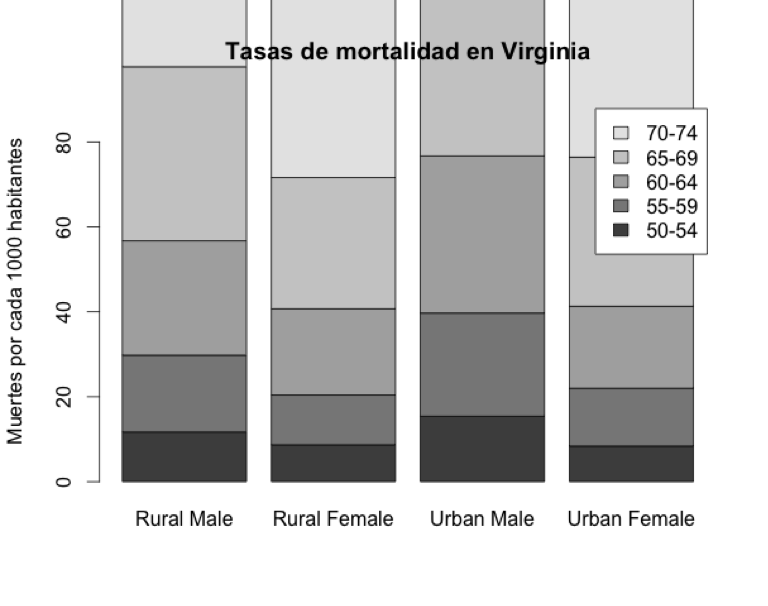
·horiz=TRUE: coloca las barras acostadas, que me parecen mucho más difíciles de leer que las barras verticales

> barplot (VADeaths,beside=TRUE, horiz=TRUE, legend=TRUE,ylim=c(0,90), ylab="Muertes por cada 1000 habitantes", main="Tasas de mortalidad en Virginia")

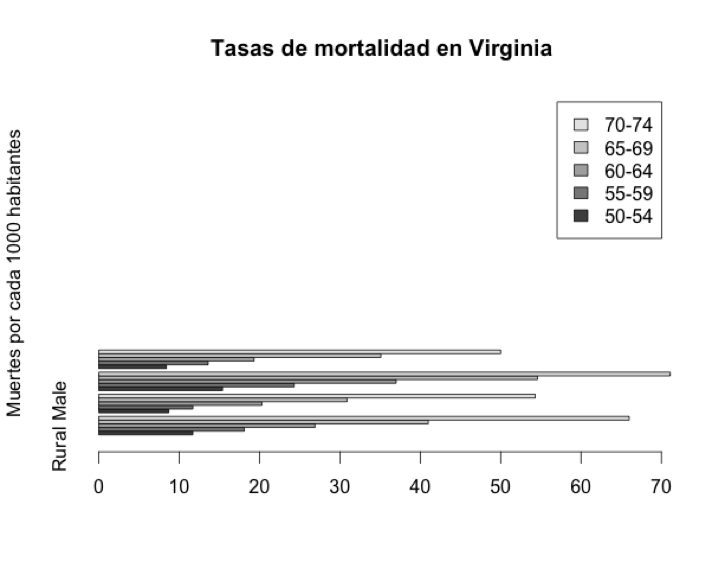
Lo que les recomiendo para adquirir más destreza es jugar con las funciones gráficas de R cuando estén usando alguna en particular, y así muy rápidamente aprenderán todo lo que les permite hacer esa función, y sobre todo verán de primera mano la mejor forma de representar sus datos. Elegir el tipo de gráfico para representar sus datos puede llegar a ser casi un arte, sobre todo para datos complejos, pero la única forma de desarrollar un criterio para hacerlo es simplemente jugando con las funciones y todas sus opciones, y ver que va saliendo.

Ahora vamos a representar los mismos datos usando un grafico de puntos (dot plot) para que vean la diferencia con el gráfico de barras:

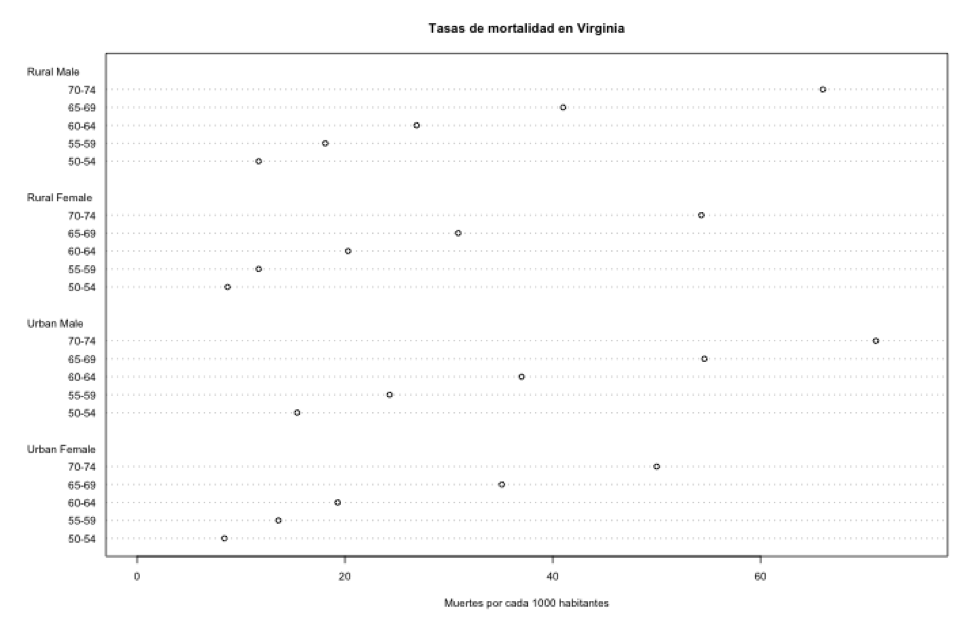
Pregunta: ¿Qué tipo de gráfico les parece mejor opción para representar los datos de mortalidad en Virginia?

Yo, personalmente, prefiero el gráfico de barras, aunque si bien no hay grandes diferencias entre hombres, mujeres, o si viven en el campo o en la ciudad, los puntitos en el diagrama de puntos están muy dispersos para seguirlos con la vista, mientras que las barras son más fáciles de comparar a simple vista.

También dense cuenta de que en este caso el gráfico de puntos no aporta gran información. Pero ahora les pido que se fijen en el gráfico de puntos del dataset mtcars (sección 2), donde representamos gráficamente una serie de modelos de coche, el número de cilindros de sus motores, y la distancia que puede recorrer cada modelo de coche por cada galón de gasolina:

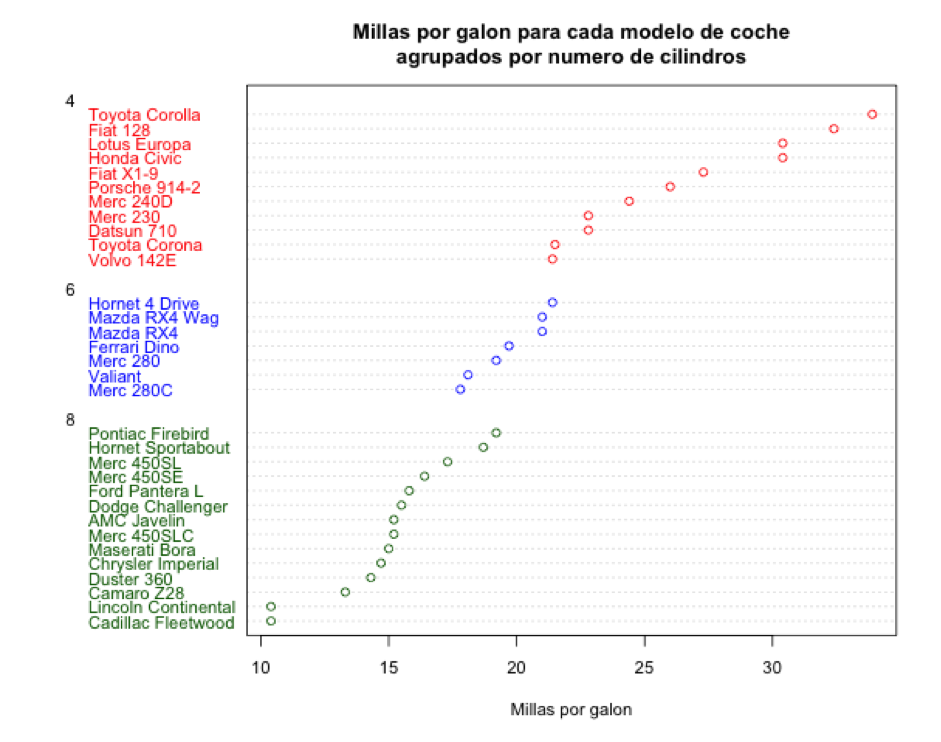
Aquí vemos que los coches con mayor número de cilindros (8) gastan más combustible (como es de esperar) que los coches con motores más pequeños, que son los coches europeos y japoneses. En este ejemplo el gráfico de puntos ofrece una visualización muy potente, pero no se me ocurre como hacerlo con la misma claridad usando un diagrama de barras. El siguiente gráfico ilustra una posibilidad de representación de mtcars usando un diagrama de barras:

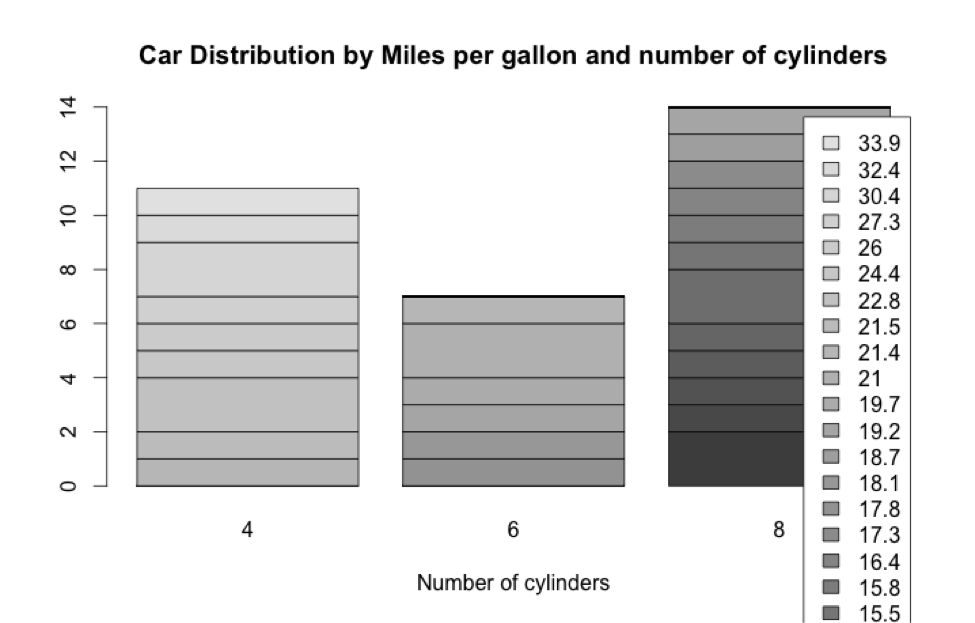
Este gráfico se ha generado con el siguiente código:

En un diagrama de barras no puedes separar a lo largo y a lo ancho porque sólo hay barras (sólo puedes crecer hacia arriba), además de que no es tan fácil agrupar las barras por valores. Por lo tanto, es muy importante jugar con los diferentes tipos de gráficos que se pueden hacer con R en el contexto de los datos específicos que tengan que representar, porque un tipo de gráfico puede ser óptimo para representar un tipo de dato determinado, pero a lo mejor no para otro.

Histogramas y gráficos de densidad kernel (kernel density plots)

Los histogramas se usan para representar la frecuencia de valores de un único tipo.

Histogramas

FUNCION PRINCIPAL: hist()

Vamos a crear un histograma con los valores de ‘Miles per galon’ del dataset mtcars.

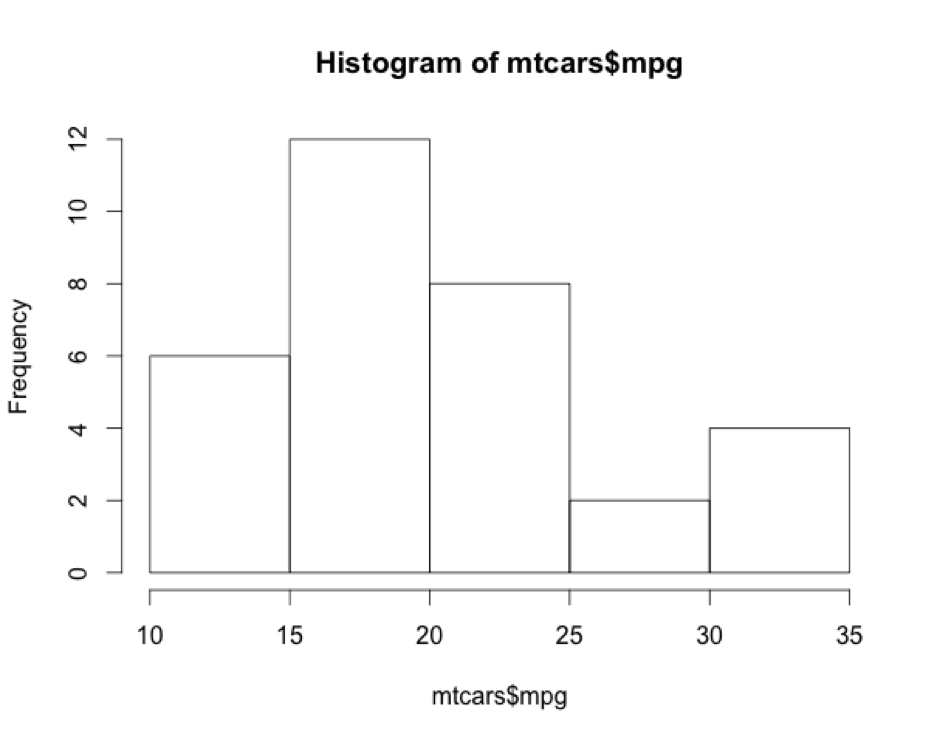
Ahora vamos a cambiar algunas opciones de la función hist():

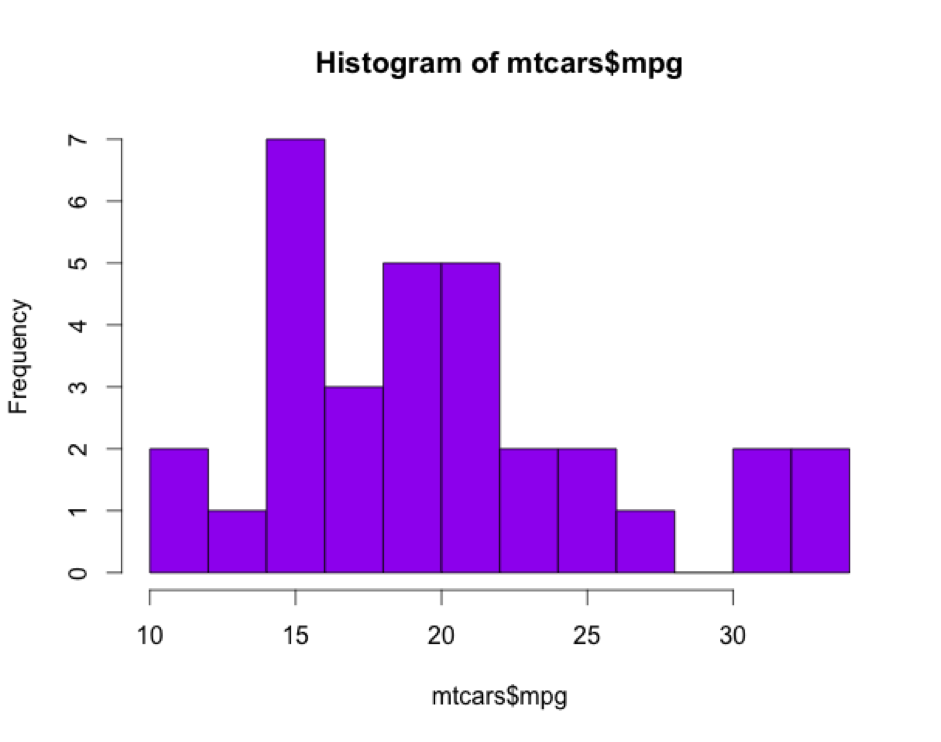
breaks=12 te indica el número de bins (compartimientos) en que divides los datos. La longitud de cada barra vertical indica la frecuencia de observaciones dentro de cada compartimiento. Lo más interesante es que R tiene una fórmula incorporada para determinar en cuantos compartimientos divide los datos de forma automática; en este caso, para las 32 observaciones de ‘Millas por galón’ R asigna los 32 datos en 5 compartimientos porque considera de forma automática que es una visualización óptima. Sin embargo, siempre llega un momento que por dividir los datos en compartimientos más y más pequeños no mejora la resolución de la visualización:

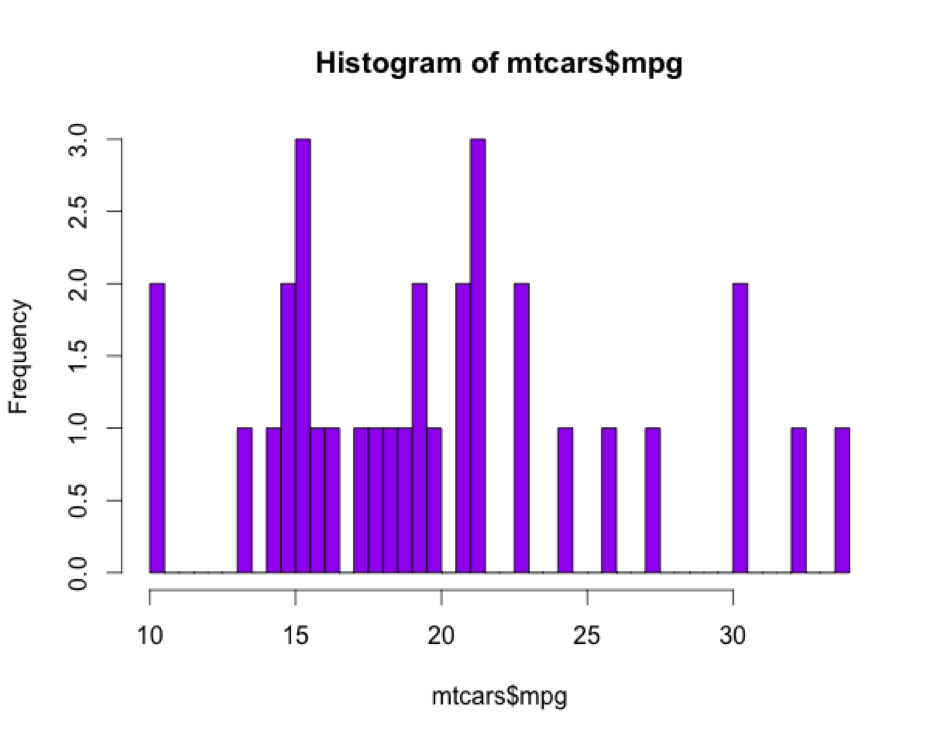
Aquí pueden ver como incluso hay compartimientos vacíos porque no tienen ningun dato en ese rango. Esto también ilustra un problema general de los histogramas, que es que en general son un método muy pobre para determinar la forma de una distribución porque el número de compartimientos afecta muchísimo a la forma. Para visualizar la forma de una distribución en vez de usar histogramas hay que usar diagramas de densidad kernel.

Diagramas de densidad kernel (kernel density plots)

FUNCIONES PRINCIPALES: plot(), polygon()

Ahora vamos a ponerle un título y a colorearlo con la función polygon().

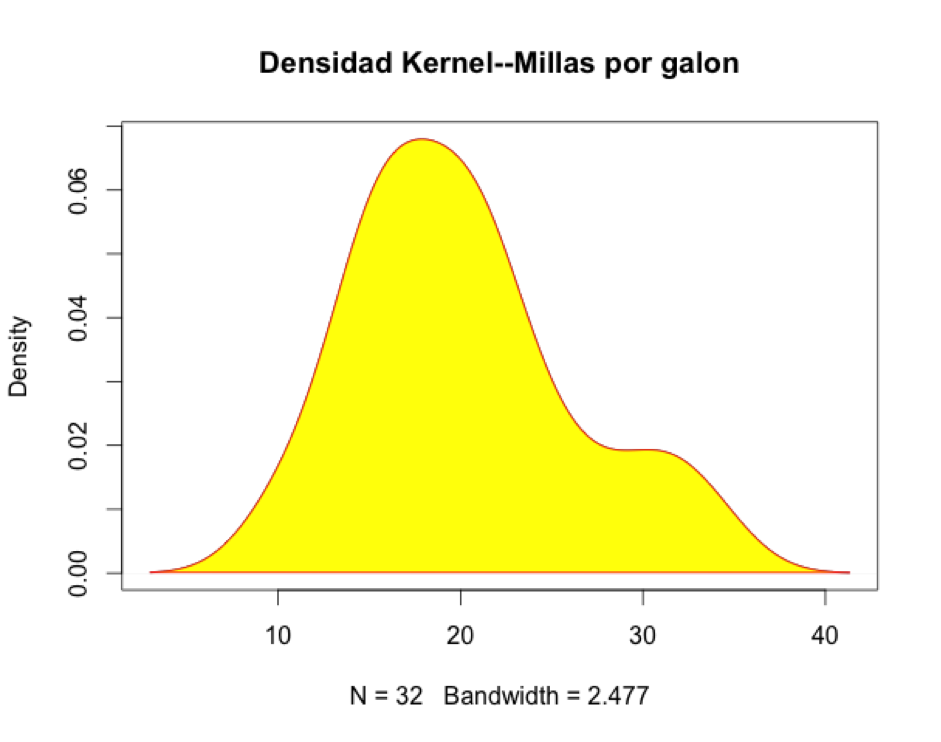
Box plots (diagramas de caja)

FUNCION PRINCIPAL: boxplot()

Los box plots (diagramas de caja) son un tipo de gráfico para representar la frecuencia de valores de un único tipo. Los box plots son una alternativa muy interesante a los histogramas porque te permiten visualizar la distribución de los datos en el contexto de variables estadísticas tan recurrentes como la mediana y los cuartiles. Vamos a usar el dataset llamado iris, que contiene una serie de medidas de las diferentes partes de una tres especies de planta. Vamos a visualizar la distribución de observaciones de la longitud de los sépalos (en cm).

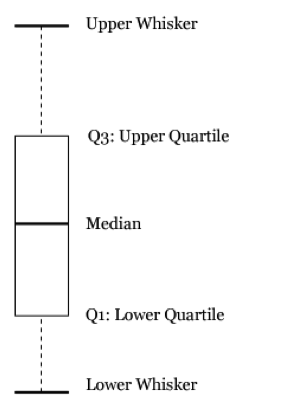
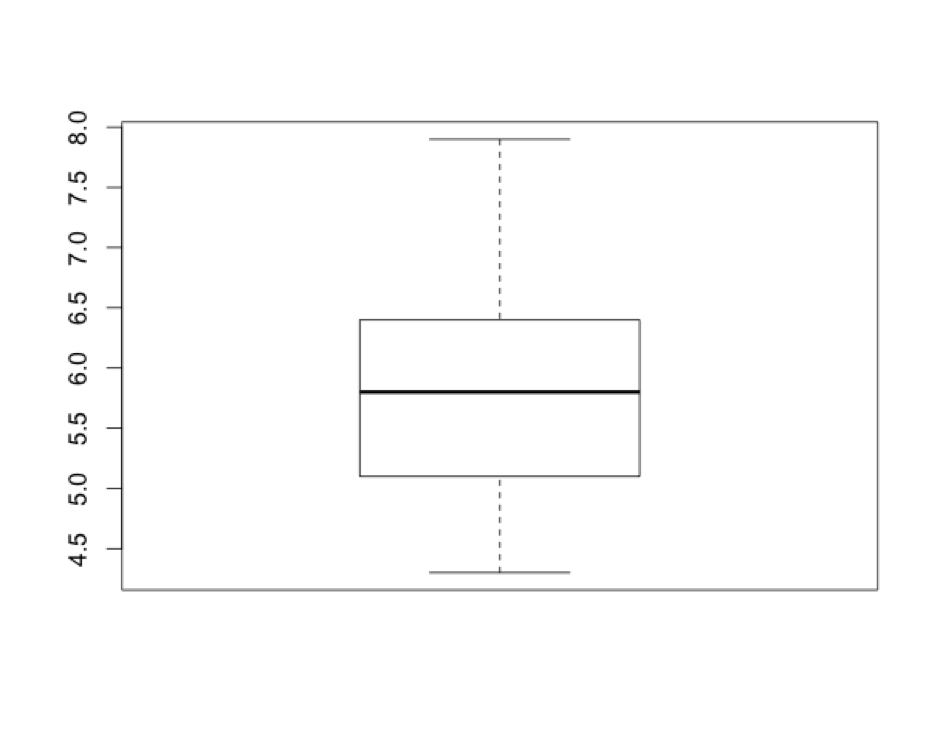Los sépalos son esas hojitas verdes que protegen a los pétalos de color que están aún dentro del capullo esperando a abrirse. Cuando el capullo de la flor termina por abrirse, los sépalos se encuentran justo en la base de los pétalos. En este diagrama, la caja delimita los valores centrales de los datos (el 50%), y las líneas que salen de la caja hacia arriba y hacia abajo (‘whiskers’ en inglés) te dan una idea de la dispersión del dataset. Propiamente dicho la caja define el rango intercuartil (el 50% central de los datos) y lo alargada que sea la caja y la longitud de los whiskers te da una idea de la dispersión de los datos. Luego los cuartiles superior e inferior representan aproximadamente el 25% de los datos mayores y menores.

Sin embargo en el dataset iris hay 3 especies de plantas diferentes, y podemos elaborar un poco más la función boxplot() para que genere un box plot para cada especie de planta.

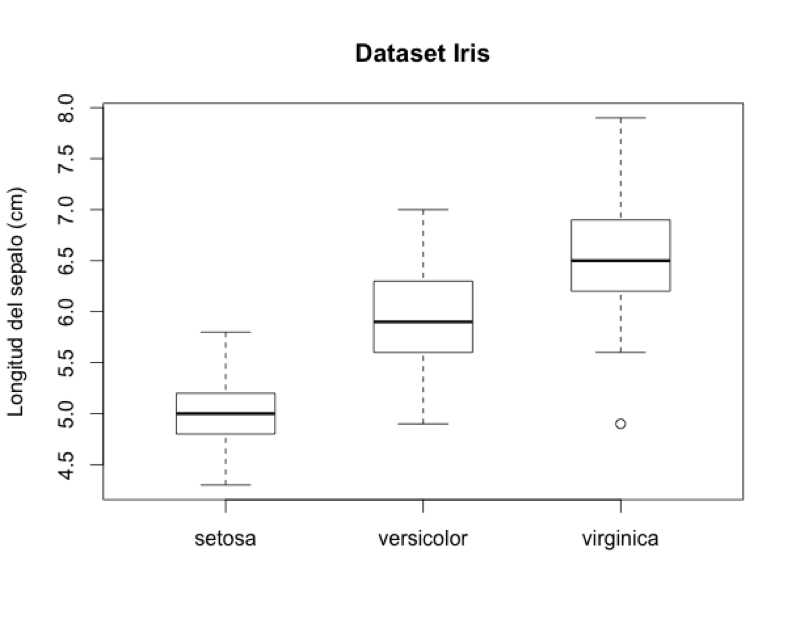
La opción boxwex te permite definir el ancho de cada caja.

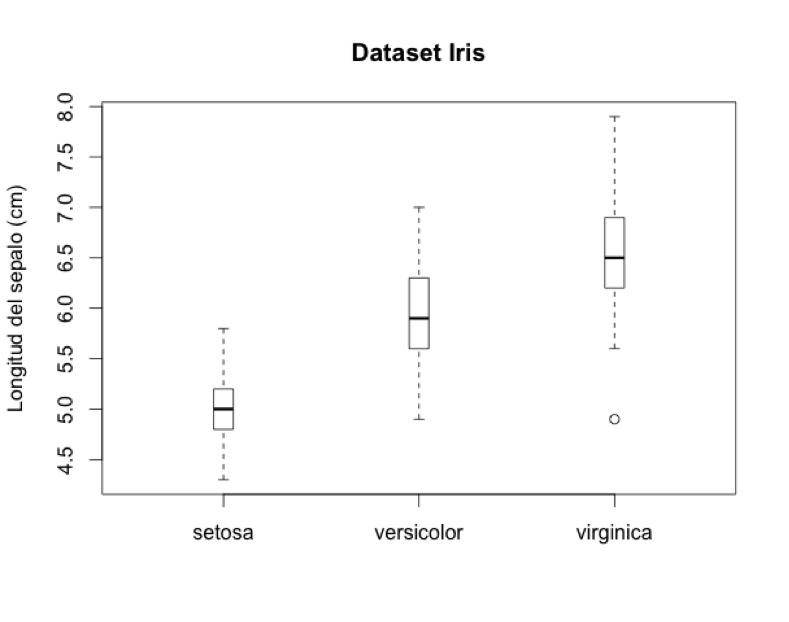
Comparación de box plots por especie

Aquí vemos que hay diferencias significativas en los tamaños de los sépalos de las plantas dependiendo de la especie de planta. Estrictamente hablando la caja más los whiskers representan el ~99% de todas las observaciones. El ~1% restante se deja para representar lo que se llaman outliers, que son observaciones muy diferentes del resto de los datos. Un ejemplo de un outlier es un especimen (planta) de la especie virginica que tiene sépalos significativamente más pequeños que los del resto de las plantas de la misma especie como para considerarla un outlier. Vamos a ver ahora de qué observación se trata:

En este caso el outlier es una observación de un sépalo de tan solo 4.9 cm de largo.

Diagramas de violín

FUNCION A INSTALAR: vioplot()

PAQUETE A INSTALAR: vioplot

Finalmente, lo último que me gustaría mencionar es que aunque un box plot te indique la dispersión de los datos y sepas el rango de valores, no te dice nada de la forma de la distribución. Es decir, que no puedes suponer que entre el principio de un whisker y el final del otro los datos que está resumiendo el box plot presentan una distribución de tipo normal o de Poisson, o de ningún otro tipo. Para combinar la potencia del boxplot con los diagramas de densidad de kernel tenemos los diagramas de violín. Vamos a hacer uno instalando primero el paquete vioplot. Separamos las observaciones de longitud de los sépalo por cada especie (virginica, versicolor y setosa).

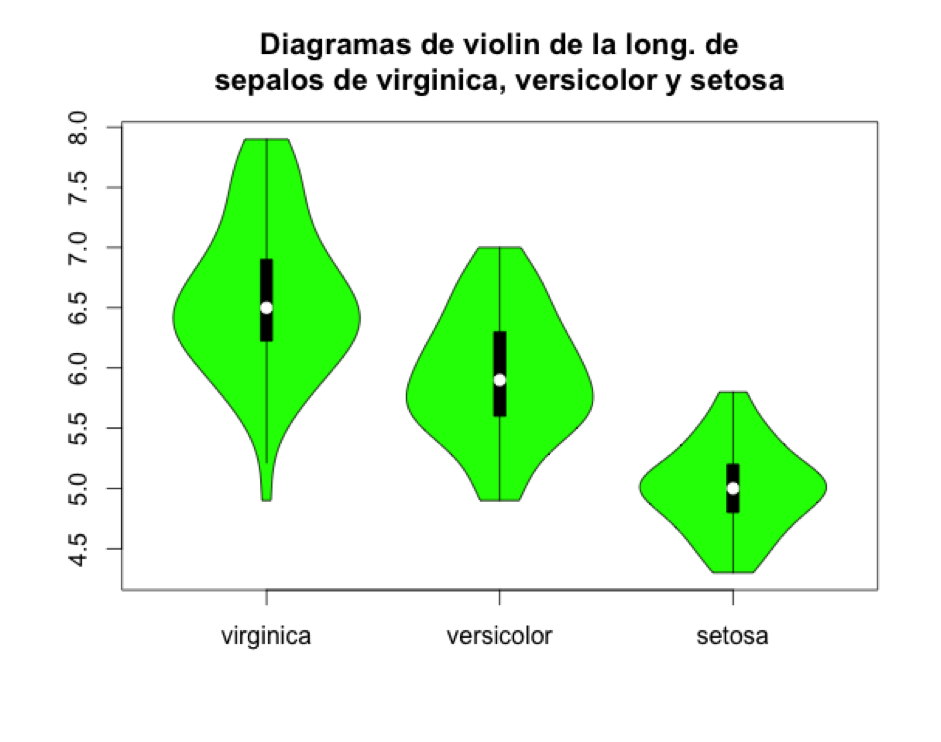
Gráficos de dispersión (scatter plots)

FUNCIONES PRINCIPALES: plot(), scatterplot3d(), plot3d()

PAQUETES A INSTALAR: scatterplot3d, rgl

Los gráficos de dispersión (scatter plots) son diagramas con ejes cartesianos (X e Y) sobre los que se visualizan valores de dos variables. También veremos como se pueden visualizar tres variables con scatter plots tri-dimensionales. La utilidad de un scatter plot donde puedes visualizar 2 variables es que te permite explorar relaciones entre las variables. A veces, antes de empezar ya sabes que existe una variable independiente (eje X) y una variable de respuesta (eje Y). Por ejemplo, si vas a una joyería a comprar un solitario, todos sabemos que el tamaño del brillante (variable independiente) está relacionado con el precio (variable dependiente), y además que la relación entre las dos variables no es lineal en toda la longitud de la comparación porque existen tan pocos diamantes de 4 o más quilates, que para las piedras muy grandes el precio se dispara más allá de lo predecible. También se puede usar un scatter plot para visualizar dos variables que no sabemos si son dependientes o no, en cuyo caso cada variable se puede representar en cualquier eje y lo que se buscaría es el grado de correlación (si existe) entre las dos variables.

            Lo primero que vamos a ver es el concepto de igualdad y diferencia cuando comparas dos datasets: ¿Qué aspecto tienen dos datasets iguales?  ¿Y dos diferentes?

Empezamos generando aleatoriamente una distribución de números normal, y otra distribución de Poisson, y visualizamos la densidad de kernel de cada una de ellas (seccion 4.2):

Ésta es una distribución normal de 100 observaciones (data points). Por definición, la distribución normal siempre está centrada en el cero (0).

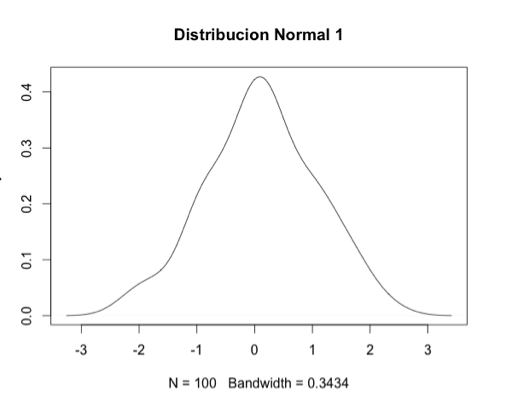
Y esta es una distribución de Poisson de 100 observaciones (data points), centrada en el número 20.

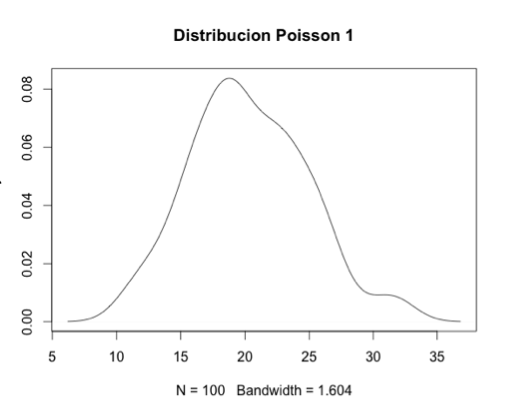
Simplemente observando estas dos distribuciones (normal y de Poisson), y sin necesidad de recurrir a un scatter plot, ya sabemos que son diferentes. ¿Pero qué aspecto tendrían dos distribuciones diferentes en un scatter plot?

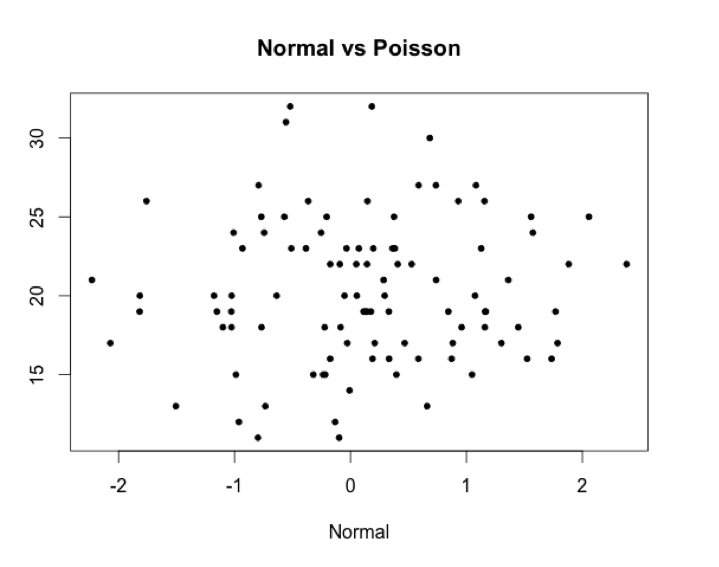
Ahora vamos a explicar en detalle cómo hace las comparaciones la funcion plot(): las dos distribuciones tienen 100 números cada una, generados aleatoriamente. Esto son 100 observaciones ordenadas en fila desde la 1ra posición hasta la numero 100. Bien, pues lo que plot() hace es comparar la equivalencia del primer data point de la distribución normal con el primer data point de la distribución de Poisson. Esto es más facil verlo si nuevamente generamos otras dos distribuciones con sólo 10 numeros cada una (aunque sea difícil justificar cualquier distribución estadística con solo 10 observaciones!):

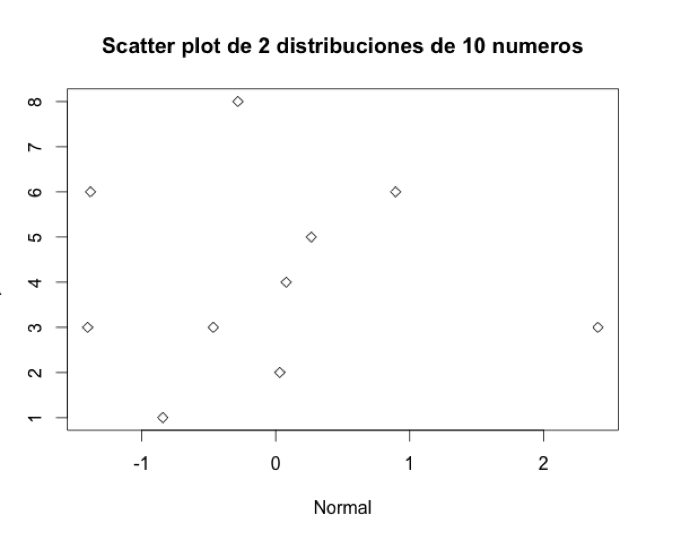
Si se fijan en el primer par de valores de las dos distribuciones (2.40439814 y 3), verán que hay un punto en el gráfico justo con estas coordenadas. Y exactamente lo mismo para los demás pares de observaciones.

Finalmente, ¿qué aspecto tendrían dos distribuciones iguales? Siempre una diagonal a 45 grados!

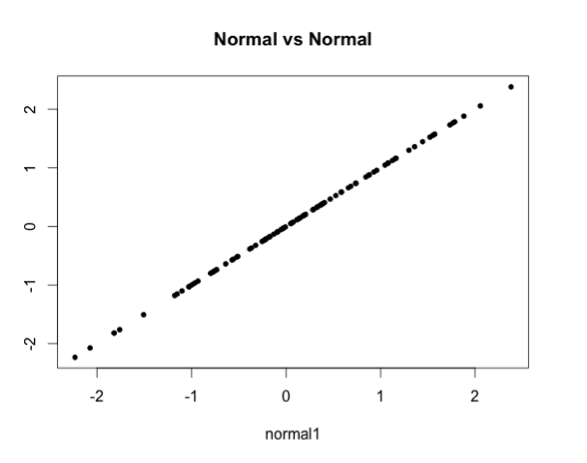
Tengan en cuenta que las distribuciones las he generado con las funciones rnorm() y rpois(), que generan números de forma aleatoria pero que encajan en la distribución de datos especificada. Por lo tanto, las distribuciones que ustedes hagan les saldrán diferentes, aunque si comparan una distribución cualquiera con ella misma, el resultado será idéntico que el que he mostrado aquí (una línea diagonal perfecta).

Ejemplos con mtcars

Vamos a visualizar la relación entre 2 variables de mtcars: el peso del coche, y las millas que puede recorrer con un galón de gasolina.

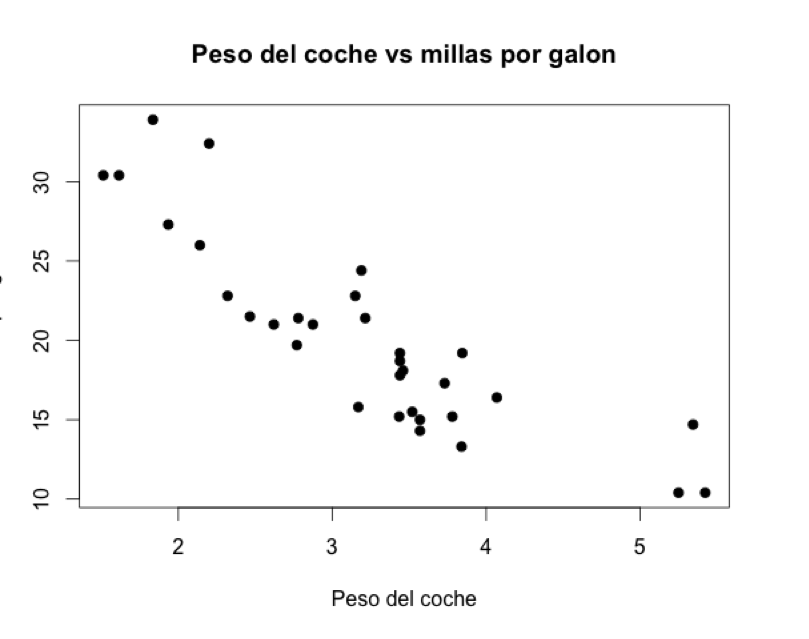
Aquí el gráfico nos está diciendo que los coches más pesados gastan más gasolina y por lo tanto les rinde menos un galón de combustible que a los coches ligeros.

Podemos seguir haciendo preguntas interesantes ya que tenemos muchos datos a mano y también las herramientas para visualizarlos. Por ejemplo, ¿habrá alguna relación entre el número de cilindros de un coche y su peso, asumiendo que los motores con más cilindros son más pesados y que por lo tanto suman bastante al peso del coche?

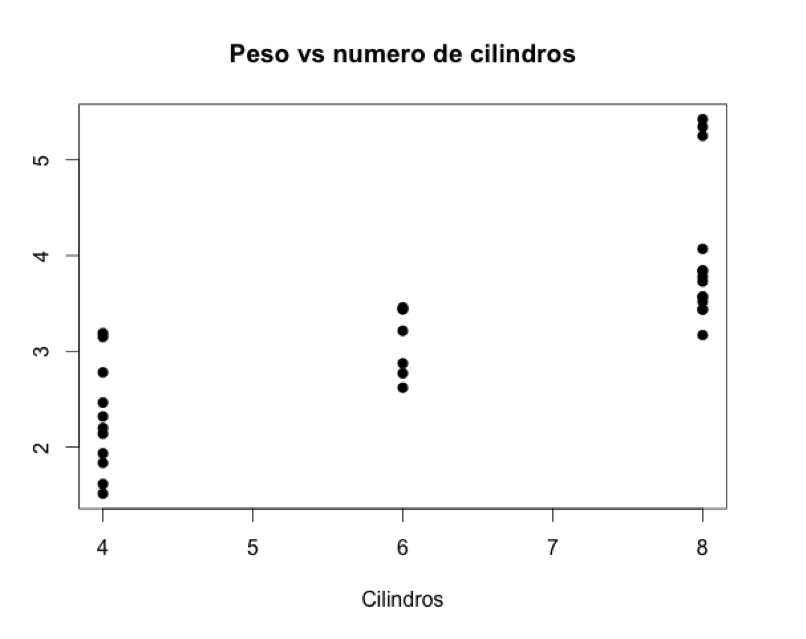
Ya sabíamos por ejemplos anteriores que en el dataset mtcars hay coches de 4, 6 y 8 cilindros, y lo que el scatter plot indica es que en general a menor número de cilindros, menor peso global del coche, y viceversa.

También podemos hacer uso del paquete scatterplot3d para visualizar en tres dimensiones tres variables diferentes (peso, cilindros y millas por galón):

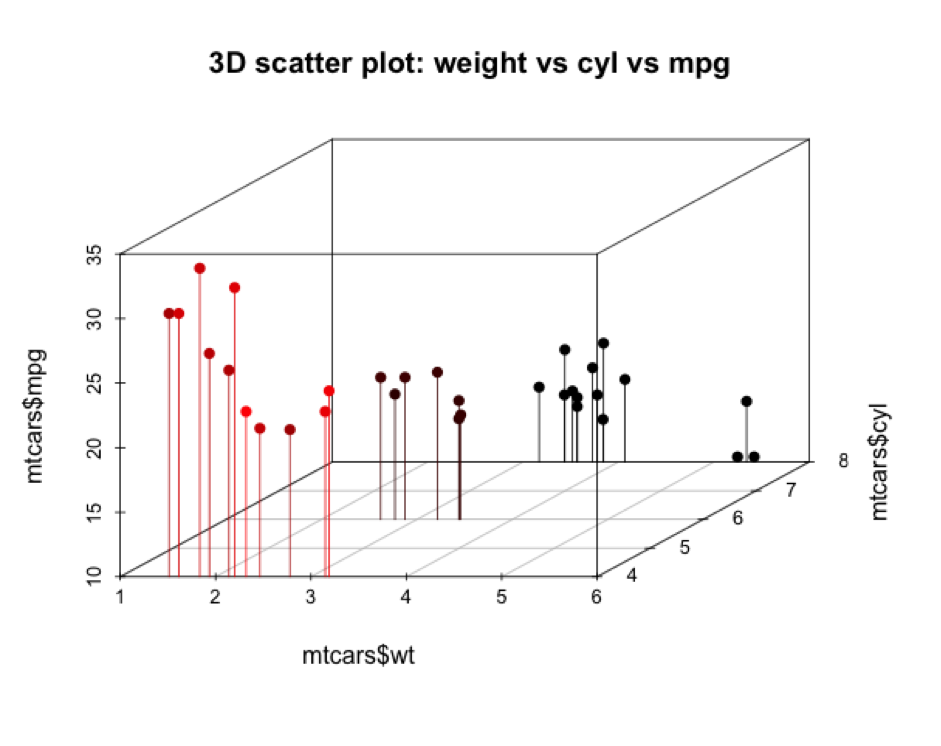
Ahora le añadimos un plano de regresión:

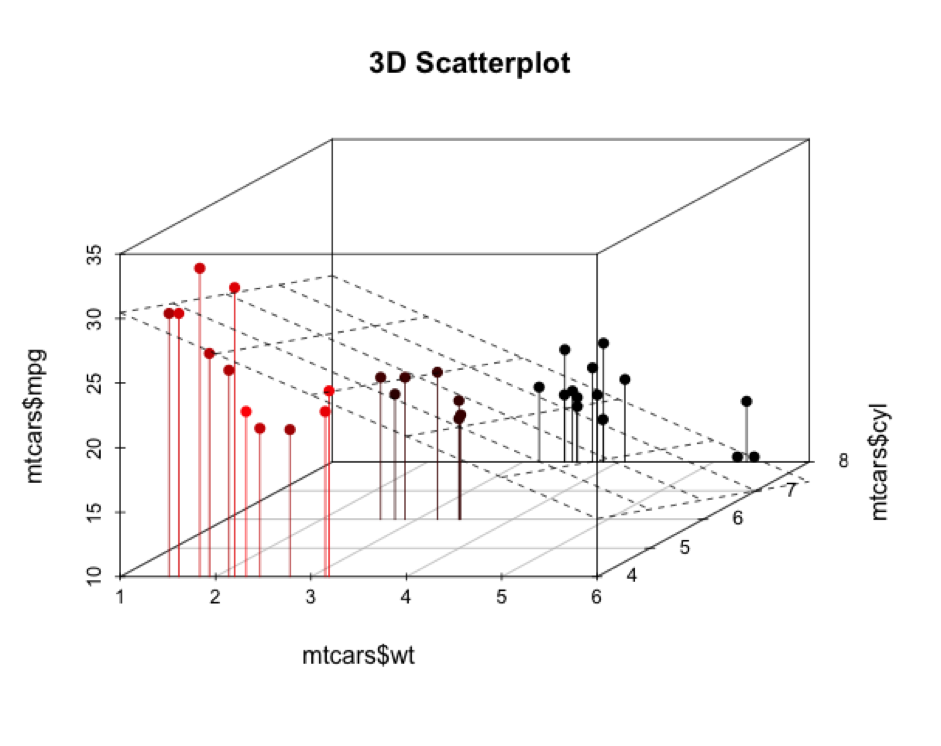
Finalmente, también podemos generar un scatter plot tridimensional interactivo que rota sobre sí mismo! Usamos el paquete rgl:

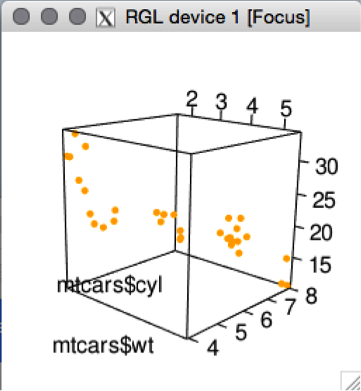
Si introducen este mismo código verán que les saldrá este cubito en una ventana aparte y que lo pueden manejar con el ratón para inspeccionarlo en 3 dimensiones!

            Los ejemplos de visualización con scatter plots que he presentado aquí ilustran sólo la punta del iceberg de lo que son las tremendas posibilidades de R a la hora de generar gráficos. Las funciones trabajadas son de las más corrientes y útiles, pero dentro de estas mismas funciones existen muchas más opciones para customizar sus gráficos que les recomiendo que exploren jugando. También existen muchas más funciones muy potentes para hacer visualizaciones más complicadas que iremos descubriendo más adelante!