05. Recursividad I
Objetivos
Los objetivos de este módulo son los siguientes:
- Revisar el concepto de recursividad visto en Fundamentos de Programación.
- Entender los principios básicos de las definiciones y métodos recursivos, y ser capaz de escribir algoritmos recursivos simples.
- Entender la diferencia entre recursividad e iteración y las ventajas de cada una de ellas.
- Comprender la diferencia entre recursividad directa e indirecta.
Introducción
En Fundamentos de Programación se introdujo el concepto de recursividad. En este módulo revisamos su definición y veremos unos cuantos ejemplos de algoritmos recursivos.
También se hará una comparativa entre las ventajas y desventajas de los algoritmos recursivos y se analizará cómo pasar un algoritmo recursivo a iterativo.
Definición
Recordemos primero que el concepto de recursividad no se reduce a algoritmos. De hecho, se dice que un elemento es recursivo cuando se define en función de sí mismo. La recursividad la podemos encontrar en muchos campos como la naturaleza, el arte y la matemáticas entre otros.
Por ejemplo, en muchas de las formas encontradas en la naturaleza podemos observar que las formas de mayor tamaño contienen copias menores, y al mismo tiempo, las menores contienen también copias de sí mismas.
También podemos ver el concepto de recursividad en las muñecas rusas o en cuadros donde el tema pintado contiene a sí mismo. Incluso en la vida cotidiana utilizamos la recursividad cuando hacemos una fotocopia de una fotocopia o una fotografía de una fotografía.
Las siguientes imágenes muestran algunos ejemplos de recursividad:
También, como se vió en Fundamentos de Programación recursividad en matemáticas se usa la recursividad para la definición de conceptos como por ejemplo:
- Los números naturales.
- Los números pares.
- El factorial de un número natural.
Otro ejemplo de matemáticas es el triángulo Sierpinski en el que cada triángulo está formado por otro más pequeños, que al mismo tiempo están formados por otros más pequeños, etc.
Como podemos ver, pues, la recursividad esté presente en nuestro entorno. Lo que queremos hacer ahora es analizar cómo se puede aplicar dicho concepto al diseño de algoritmos. ¿En qué caso se puede utilizar un algoritmo recursivo? ¿Cómo lo diseñamos y como comprobamos que funciona correctamente? Estas son algunas preguntas que nos hacemos y como vamos a ver en este módulo y en el siguiente, la dificultad de la recursividad no está en la programación en sí misma sino en el diseño de los algoritmos.
Principio de inducción
Para resolver problemas recursivos hace falta razonar de manera similar a cuando se usa el Principio de Inducción para demostraciones matemáticas sobre los números naturales.
Recordemos en que consiste el principio de inducción. Este principio se usa de la siguiente manera demostrar una propiedad de los números naturales:
- Demostrar que la propiedad es válida para el caso más simple, normalmente para el caso n = 0 (en algún caso el caso más simple puede ser otro natural como 1 ó 2).
- Demostrar que si es cierto para n también lo es para n+1.
Veamos un par de ejemplos:
Ejemplo 05_01
Demostrar que la suma de los n primeros números naturales es igual a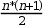 
, es decir:
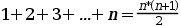
Base de inducción: hay que comprovar que la fórmula es cierta para el caso más simple, es decir para n = 1. Si sustituimos n por 1 en la fórmula tenemos:
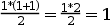
Por lo tanto podemos decir que la fórmula es cierta para el caso base n = 1.
Hipótesis de inducción: supongamos que la fórmula es cierta para n. Es decir, que ...
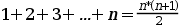
... es cierto.
Demostración: ahora debemos demostrar que también es cierto para n+1.
Cómo lo planteamos? Sabemos que ...
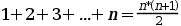
... es cierto y hemos de demostrarlo para n+1, es decir queremos ver si también es cierto que:
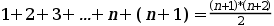
Como hemos supuesto que para n la fórmula es cierta, podemos hacer la siguiente sustitución:
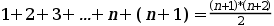
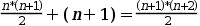
Y haciendo operaciones nos queda:
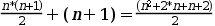
Operando en la parte izquierda nos queda:
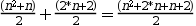
Y podemos ver que tanto la expresión en la parte izquierda como en la derecha son iguales.
Comentarios
La inducción funciona de tal manera que tenemos un caso base que podemos demostrar que es cierto. Luego demostramos que si es cierto para n lo es para n+1.
Por lo tanto tenemos que:
- Es cierto per n = 1 (demostrado).
- Como es cierto que para n = 1, aplicando la inducción sabemos que es cierto para n = 2.
- Como es cierto que para n = 2, aplicando la inducción sabemos que es cierto para n = 3.
- Etc. Siguiendo con el razonamiento podemos decir que la propiedad es cierta para todo número natural.
Ejemplo 05_02
Supongamos que queremos demostrar:
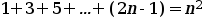
Usamos el principio de inducción para demostrarlo.
Base de inducción
Debemos demostar que es cierto para n = 1. Si sustituimos n por 1 en la fórmula tenemos:
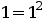
Que claramente es cierto.
Hipótesis de inducción
Suponemos que es cierto para n, es decir que ...
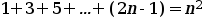
... es cierto.
Demostración
Ahora debemos demostrar que es cierto para n+1. Para ello escribimos la fórmula para n+1. Sería:
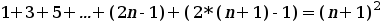
Utilizamos la hipótesis de inducción y escribimos:
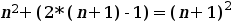
Si operamos a ambos lados obtenemos:
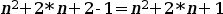
Que resulta:
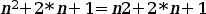
O sea que hemos demostrado que la fórmula es cierta.
Principios de los algoritmos recursivos
La recursividad se basa en la inducción. Al igual que en el principio de inducción, para un algoritmo recursivo necesitamos un caso base, que hará que la recursividad se pare. El caso base debe ser aquel para el que sabemos exactamente su resultado. Y el caso recursivo, donde se define el término n-ésimo en función de los anteriores.
Por ejemplo:
- Para el factorial sabemos que 1! = 1, y para el resto n! = n*n(-1).
- Para la serie de Fibonacci sabemos que fib(1)=1 i fib(2)=1 y para el resto fib( n )= fib(n-1) + fib(n-2).
- Para una multiplicación a*b, si b=1 sabemos que a*1 = a para el resto es a*(b-1)*b.
A continuación vamos a ver unos cuantos ejemplos de algoritmos recursivos.
Ejemplo 05_03: palíndromos
Vamos a ver cómo podemos escribir un algoritmo recursivo que comprueba si uan cadena de caracteres forma un palíndromo o no. Recordemos que un texto forma un palíndromo si se lee igual de izquierda a derecha que de derecha a izquierda. Algunos ejemplos palíndromos:
- Madam, I’m Adam.
- A global rotator lab, Olga.
- Revenge Meg, never!
- Dábale arroz a la zorra el abad.
- O Rey o Joyero.
Para decidir si una cadena de caracteres es un palíndromo hay que primero quitar los blancos y signos de puntación así como los acentos.
Para resolver el problema es fácil ver que podemos hacerlo de forma recursiva. Hacemos lo siguiente:
- Si la cadena tiene un único carácter o está vacía es un palíndromo.
- Si el primer y último carácter son diferentes ya sabemos que no lo es. En caso contrario lo será si la subcadena resultante de extraer el primer y último carácter también lo es.
Ya tenemos una definición recursiva. Vamos a formalizarla:
Caso base: mirar la longitud de la cadena. Si es 0 o 1 retornar cierto.
Recursión: mirar si los extremos son iguales. Si lo son retornamos el valor resultante de analizar la subcadena sin los extremos. En caso contrario retornamos falso.
Vamos a ver cómo escribimos el algoritmo:
Definimos primero el tipo de datos. En este caso vamos a usar una tabla de caracteres para guardar la cadena. También se podría usar otro tipo de datos para resolverlo. Definimos:
const
MAX_LETTERS: integer = 200;
end const
type
tSentence = record
sentence: array [MAX_LETTERS] of char;
numChars: integer;
end record
end type
#define MAX_LETTERS 200
typedef enum {FALSE, TRUE} boolean;
typedef struct {
char *sentence;
int numChars;
} tSentence;
Decidimos ahora la cabecera de la función recursiva. La solución no es única, pero en nuestro caso optaremos por pasar siempre la cadena completa y dos enteros para indicar el principio y fin de la subcadena que se quiere analizar.
La cabecera quedará:
function isPalindrome(sentence: tSentence, posIni: integer, posFinal: integer): boolean;
boolean isPalindrome(tSentence sentence, int posIni, int posFinal);
Caso base: las condiciones que harán parar la recursividad están relacionadas con la longitud de la cadena. Si ésta es 1 podremos afirmar que es un palíndromo. Por defecto també consideraremos palíndromo el caso en que la cadena sea vacía.
Recursión: retornar el resultado de comparar los extremos y el resultado de llamar recursivamente a sí misma sin los extremos.
La función queda:
function isPalindrome(sentence: tSentence, posIni: integer, posFinal: integer): boolean
if posIni ≥ posFInal then
return true;
else
return sentence.sentence[posIni] = sentence.sentence[posFInal] and isPalindrome(sentence, posIni+1, posFinal-1))
end if
end function
boolean isPalindrome(tSentence sentence, int posIni, int posFinal) {
if (posIni >= posFinal) {
return TRUE;
} else {
return (sentence.sentence[posIni] == sentence.sentence[posFinal]) && isPalindrome(sentence, posIni+1, posFinal-1);
}
}
Ahora falta definir el programa principal que hará la primera llamada a isPalindrome. Para simplificar el ejemplo, supondremos que la cadena entrada ya no tiene ni blancos ni signos de puntuación ni vocales acentuadas. En el caso que no fuera así sería necesario llamar primero a una función que "limpiase" la cadena.
const
MAX_LETTER: integer = 200;
end const
type
tSentence = record
sentence: array [MAX_LETTERS] of char;
numChars: integer;
end record
end type
algorithm palindrome
var
sentence: tSentence;
end var
writeString("Enter and alphabetical string with no blanks");
sentence.sentence = readString();
sentence.numChars = length(sentence.sentence);
if isPalindrome(sentence, 1, sentence.numChars) then
writeString("It is a palndrome")
else
writeString("It is not a palindrome");
end if
end algorithm
function isPalindrome (sentence: tSentence, posIni: integer, posFinal: integer): boolean
if posIni ≥ posFInal then
return true;
else
return sentence.sentence[posIni] = sentence.sentence[posFInal] and isPalindrome(sentence, posIni+1, posFinal-1);
end if
end function
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <string.h>
#define MAX_LETTERS 200
typedef enum {FALSE, TRUE} boolean;
typedef struct {
char *sentence;
int numChars;
} tSentence;
boolean isPalindrome(tSentence sentence, int posIni, int posFinal);
int main(void) {
tSentence sentence;
sentence.sentence = malloc(MAX_LETTERS*sizeof(char));
printf("Enter and alphabetical string with no blanks\n");
scanf("%[^\n]", sentence.sentence);
fflush(stdin);
sentence.numChars = strlen(sentence.sentence);
if (isPalindrome(sentence, 0, sentence.numChars-1)) {
printf("It is a palindrome");
} else {
printf("It is not a palindrome");
}
return 0;
}
boolean isPalindrome(tSentence sentence, int posIni, int posFinal) {
if (posIni >= posFinal) {
return TRUE;
} else {
return (sentence.sentence[posIni] == sentence.sentence[posFinal]) && isPalindrome(sentence, posIni+1, posFinal-1);
}
}
El dibujo siguiente muestra la secuencia de llamadas que hará la función isPalindrom si utilizamos la cadena "revengemegnever":
Ejemplo 05_04: potencia de dos números
Una manera de calcular la potencia de dos naturales es de la siguiente manera:
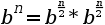si n es par.
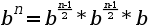si n es impar
Aplicando esta definición podemos escribir una función recursiva que calcule la potencia.
function power(base: integer, exp: integer): integer
var
temp: integer;
end var
if exp = 1 then
return base;
else
if exp mod 2 = 0 then
temp = power(base, exp div 2);
return temp*temp;
else
temp = power(base, (exp-1) div 2);
return temp*temp*base;
end if
end if
end function
algorithm computePower
var
base: integer;
exp: integer;
end var
base := readInteger();
exp := readInteger();
writeInteger(power(base, exp));
end algorithm
#include <stdio.h>
int power(int base, int exp);
int main(void) {
int base;
int exp;
scanf("%d", &base);
scanf("%d", &exp);
printf("%d\n", power(base, exp));
return 0;
}
int power(int base, int exp) {
int temp;
if (exp == 1) {
return base;
} else if (exp%2 == 0) {
temp = power(base, exp/2);
return temp*temp;
} else {
temp = power(base, (exp-1)/2);
return temp*temp*base;
}
}
La secuencia de llamadas que se harán si calculamos 2 a la 10 será la siguiente:
power(2,10)
power(2,5)
power(2,2)
power(2,1)
return 2
return 2 * 2
return 4 * 4 * 2
return 32 * 32
Ejemplo 05_05: serie de Fibonacci
En este ejemplo veremos un caso en el que la solución recursiva, aunque elegante, no es muy eficiente.
Calcular un elemento de la serie de Fibonacci recursivamente es fácil y elegante, ya que la propia definición de la serie lo es. Recordemos la definición:
- Si n = 1 entonce f(1) = 1.
- Si n = 2 entonce f(2) = 1.
- Para cualquier otro valor n f( n ) = f(n-1) + f(n-2).
En este caso la definición ya nos da el caso base para los valores de n igual a 1 y 2, y también la propia definición de la recursividad.
La implementación recursiva quedaría de la siguiente manera:
algorithm fibonacci
var
n: integer;
result: integer;
end var
writeString("Enter a positive integer number");
n := readInteger();
result:= fib( n );
writeString("the n-th element of the Fibonacci series is:");
writeInteger(result);
end algorithm
function fib(n: integer)
if n=1 or n=2 then
return 1;
else
return (fib(n-1) + fib(n-2));
end if
end function
#include <stdio.h>
#include <conio.h>
int fib(int n);
int main(void) {
int n;
int result;
printf("Enter a positive integer number");
scanf("%d", &n);
result = fib( n );
printf("The n-th element of the Fibonacci series is: %d\n", result);
return 0;
}
int fib(int n){
if (n==1 || n==2) {
return 1;
} else {
return (fib(n-1) + fib(n-2));
}
}
El algoritmo es fácil de entender pero es muy poco eficiente. Por ejemplo, para calcular fib( n ) hace falta calcular fib(n-1) y fib(n-2), pero para calcular fib(n-1) vuelve a ser necesario calcular fib(n-2).
En el dibujo siguiente se pueden ver las llamadas que se harían usado el algoritmo recursivo en el caso de n=5. Para cada paso se hacen dos llamadas menos cuando se llega a n=1 o n=2 que retorna directamente 1. Como podemos ver, se realizan llamadas repetidas haciendo que el algoritmo no sea eficiente.
En este caso es mejor utilizar un algoritmo iterativo que calcule el término de Fibonacci de una manera incremental.
Ejemplo 05_06: como invertir las cifras de un número natural
Supongamos que nos piden un algoritmo que invierta las cifras de un número natural. Lo primero que podemos pensar es una solución iterativa, pero también hay una solución recursiva, aunque no es evidente de entrada.
Veamos primero la siguiente tabla que nos puede dar una pista de como diseñar el algoritmo.
Es decir, si tenemos el número 1234567, por ejemplo, lo que se debe hacer es lo siguiente:
| Paso | Número original | Número mod 10 | Construcción del número invertido | Comentario |
|---|---|---|---|---|
| 1 | 1234567 | 7 | 0*10 + 7 = 7 | Cogemos el número que estamos construyendo, de momento 0, lo multiplicamos por 10 y le sumamos la última cifra del número original |
| 2 | 123456 | 6 | 7*10 + 6 = 76 | Repetimos la operación anterior |
| 3 | 12345 | 5 | 76*10 + 5 =765 | Repetimos la operación anterior |
| 4 | 1234 | 4 | 765*10 + 4 = 7654 | Repetimos la operación anterior |
| 5 | 123 | 3 | 7654*10 + 3 = 76543 | Repetimos la operación anterior |
| 6 | 12 | 2 | 76543*10 + 2 = 765432 | Repetimos la operación anterior |
| 7 | 1 | 1 | 765432*10 + 1 = 7654321 | Repetimos la operación anterior |
| 8 | 0 | 0 | Se acaba el proceso |
Por lo que vemos, el inverso lo vamos construyendo a medida que se van haciendo las llamadas recursivas. Es necesario hacerlo así ya que la cifra menos significativa hay que extraerla y multiplicarla por una potencia de 10 que a priori no sabemos cuál es. Si en cada llamada la multiplicamos por 10, al final la cifra menos significativa ocupará el lugar que le toca en el número invertido.
Por lo tanto definiremos una función a la que le pasaremos dos parámetros, el número que queremos invertir y el que vamos construyendo. Cuando se llegue al final de la recursividad devolveremos el número que se ha ido construyendo en cada llamada.
La cabecera de la función será:
function reverse(number: integer, temp: integer): integer
int reverse(unsigned int number, unsigned int temp);
Caso base: será cuando el número a invertir sea 0 (ya no quedan cifras). Cuando ya no quedan la función retorna el segundo parámetro, que es el inverso.
Recursión: llamamos a la función recursiva pasando como primer parámetro el número al que le hemos quitado la cifra menos significativa (number div 10) y como segundo el que vamos construyendo.
function reverse(number: integer, temp: integer): integer
if number = 0 then
return temp;
else
return reverse(number div 10, temp*10 + number mod 10);
end if
end function
algorithm reverseRec
var
num, result: integer;
end var
num := readInteger();
writeInteger(reverse(num, 0));
end algorithm
unsigned int reverse(unsigned int number, unsigned int temp) {
if (number==0) {
return temp;
} else {
return reverse(number/10, temp*10 + number%10);
}
}
int main(void) {
unsigned int num;
unsigned int result;
printf("Write a natural numbrer: ");
scanf("%d", &num);
result = reverse(num, 0);
printf("%d\n", result);
return 0;
}
Resumen
En esta unidad hemos revisado el concepto de recursividad y lo hemos comparada con el principio de Inducción matemática.
Hemos visto que todo algoritmo recursivo debe tener un caso base para parar la recursividad y el caso recursivo que resuelve el problema llamándose a sí mismo.
En la siguiente unidad continuaremos con la recursividad. Analizaremos los diferentes tipos de recursividad, veremos como pasar un algoritmo recursivo a iterativo y veremos algún ejemplo más de algoritmos recursivos.