02. Especificación formal de algoritmos
Objetivos
Los principales objetivos de este módulo son los siguientes:
- Entender que significa especificar un problema.
- Distinguir entre especificación de un problema (qué debe resolver) y algoritmo (cómo se debe resolver).
- Comprender cuales son los elementos de una especificación: variables de entrada y salida, precondición y postcondición.
- Aprender cuales son los elementos básicos del lenguaje formal de predicados para especificar problemas.
- Saber especificar problemas sencillos.
Introducción
En la asignatura de Fundamentos de Programación visteis los componentes de los lenguajes de programación (algoritmo y C) que permiten escribir algoritmos para resolver los problemas concretos.
Ahora bien, el punto de partida para escribir un algoritmo es precisamente la descripción del problema que se quiere resolver. Esta tarea, que podría parecer sencilla, no siempre lo es ya que normalmente se utiliza el lenguaje natural para describir el problema, y el lenguaje natural, por falta de formalidad, puede introducir ambigüedades y falta de claridad en la descripción de los problemas. Esta ambigüedad puede provocar el desarrollo de algoritmos erróneos y, por lo tanto, una pérdida de tiempo en la resolución final de los problemas.
Una manera de asegurar que el enunciado es claro es utilizar un lenguaje formal para escribir el enunciado. Describir un problema y el resultado esperado de manera formal se llama especificar el problema. Este módulo trata de la especificación, define los conceptos básicos introduce el lenguaje formal utilizado para especificar y proporciona algunos ejemplos de cómo especificar problemas sencillos.
Aproximación intuitiva
Imaginemos que unos padres contratan a una canguro para llevar los hijos al colegio.
El problema a resolver podría ser: recoger a los niños a las 8:00 de la mañana y llevarlos al colegio.
Si el encargo que hacen a la futura canguro no se detalla más, la canguro se puede encontrar con sorpresas. Por ejemplo, estarán los niños vestidos y preparados para salir o hará falta vestirlos? A qué hora deben llegar al colegio? Estos detalles son importantes para poder cumplir con éxito la tarea encomendada.
La canguro, para poder preparar su algoritmo (solución del problema que consiste en identificar las acciones que debe hacer para llevar los niños al colegio y llegar puntual) debe saber, entre otras cosas, cómo los encontrará y a qué hora deben llegar al colegio. Se debe formalizar el punto de partida del problema y la situación final.
Por lo tanto se debería especificar el problema. Eso quiere decir indicar claramente la situación de partida y la situación final.
Una posible solución sería:
En el dibujo podemos ver en el recuadro de la izquierda como se especifica la situación inicial del problema. Dice que la situación de partida correcta es que la canguro debe encontrará a los niños listos para marchar. Por otro lado, el recuadro de la derecha indica cuál debe ser la situación final: los niños deben estar en la puerta del colegio antes de las 8:30 de la mañana.
Hay que fijarse que en ningún momento se le dice cómo debe ir a la escuela: la manera de ir se deja a criterio de la canguro. Es decir, la especificación no indica cómo resolver el problema sino la situación inicial y la final. Hay que remarcar que lo que describe la especificación es el cambio de estado del entorno. En este caso, el entorno está formado por los niños y dónde se encuentran. El cambio de entorno hace que los niños pasen de estar en casa a estar en el colegio.
En un entorno de programación, el entorno es el conjunto de variables de entrada y salida del problema. Las variables que se puedan utilizar durante la resolución no forman parte de la especificación sino de la resolución. La especificación indicará cómo ha de cambiar el entorno: situación inicial y final.
Elementos de la especificación
En el apartado anterior hemos visto de manera informal en qué consistía la especificación de un problema. Ahora vamos a formalizar su definición.
La especificación de un algoritmo consta de cuatro partes:
- Elementos que definen el entorno: declaración de las variables de entrada y salida.
- Precondición: estado inicial del entorno.
- Nombre del algoritmo.
- Postcondición: estado final del entorno.
Variables: declaración de las variables necesarias para especificar el problema. Como ya hemos dicho serán esas variables sobre las que definiremos las condiciones tanto de entrada como de salida. Para cada variable indicaremos su nombre y su tipo. Los nombres de las variables deben ser significativos.
Precondición: definición de la condición que debe cumplirse al inicio del algoritmo. Cuáles son los valores válidos de las variables de entrada.
Nombre del algoritmo: identificación del algoritmo mediante el nombre que estamos especificando. Debería ser lo más significativo posible.
Postcondición: definición de la condición que se debe cumplir al final del algoritmo. Son las condiciones sobre los posibles valores finales de las variables.
Ejemplo 02_01
Supongamos que nos piden especificar un algoritmo que dado un entero n positivo, calcule la suma de los n primeros cuadrados:
Variables: los datos de entrada se reducen en este caso a una única variable necesaria para representar al entero, la llamaremos number y para la salida necesitamos otro entero para guardar el resultado, la llamaremos sum. Escribimos lo siguiente:
var
number: integer;
sum: integer;
end var
int sum;
Precondición: debe indicar el estado inicial del entorno que permita que el algoritmo se ejecute correctamente y devuelva el valor esperado. En este caso hemos definido una variable de tipo entero, number, como variable de entrada. Podríamos escribir que number debe de ser un entero positivo, utilizando lenguaje natural, pero en la especificación queremos evitar el lenguaje natural. Utilizando un lenguaje más formal podemos escribir:
{ Pre: number = NUMBER ʌ NUMBER > 0 }
Por qué escribimos number = NUMBER? Tenemos que tener en cuenta que number es una variable y su valor puede cambiar durante la ejecución del algoritmo. Cuando escribamos la postcondició haremos referencia al valor inicial de la variable number. La forma de indicar el valor inicial es mediante:
number = NUMBER
Nombre del algoritmo: buscamos un nombre representativo de lo que hace el algoritmo. En este caso podríamos poner, por ejemplo:
sumaCuadrados
Postcondición: debe indicar el estado final del entorno. Lo hacemos indicando cuál debe ser el valor correcto de la variable de salida, en este caso sum. Si utilizamos lenguaje natural diríamos que debe ser la suma de los cuadrados de los números 1 hasta NUMBER. En lenguaje formal escribimos:
{ Post: 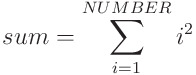 }
}
Fijaros que utilizamos NUMBER para indicar hasta dónde debemos sumar. No podemos utilizar el nombre de la variable number porque durante la ejecución puede haber cambiado su valor.
Cálculo de predicados
En el apartado anterior, hemos dicho que las precondiciones y postcondiciones describen formalmente y de manera no ambigua el estado del entorno antes y después de la ejecución de un algoritmo y hemos visto un ejemplo.
La pregunta es ahora que lenguaje se debe utilizar para especificar formalmente. Sabemos que el lenguaje natural no siempre es el adecuado para una escritura formal de las precondiciones y postcondiciones, ya que es fácil introducir ambigüedad y es difícil ser formal al escribirlas.
Una manera de hacerlo formalmente es usando el cálculo de predicados.
En este apartado recordaremos los componentes básicos del cálculo de predicados que nos permiten escribir precondiciones y postcondiciones de manera formal.
Recordemos primero qué es un predicado: es una expresión booleana en la que pueden aparecer variables.
Los siguientes son ejemplos de predicados válidos:
- 3+6 > 15, que tiene siempre el valor falso, ya que 9 no es mayor que 15.
- edad = 45, que puede tener el valor cierto o falso dependiendo del valor que tenga la variable edad. Si edad tiene el valor 45 el resultado será cierto, en caso contrario será falso.
- edad*3 > 78, que puede tener el valor cierto o falso dependiendo del valor que tenga la variable edad. Si edad tiene un valor mayor que 26 el resultado será cierto, en caso contrario será falso.
Un predicado puede estar formado por:
- constantes: 3, 89, 75, etc.
- variables: edad, año, dia, etc.
- operadores aritméticos:
| símbolo | nombre | se lee como |
| + | suma | más |
| - | resta | menos |
| * | multiplicación | por |
| / | división | dividido |
| div | división (parte entera) | parte entera de la división |
| mod | división (residuo) | residuo de la división |
| ∑ | sumatorio | suma desde ... hasta ... |
- operadores relacionales:
| símbolo | nombre | se lee como |
| < | desigualdad | es menor que |
| ≤ | desigualdad | es menor o igual que |
| > | desigualdad | es mayor que |
| ≥ | desigualdad | es mayor o igual que |
| = | igualdad | es igual que |
| ≠ | desigualdad | es distinto que |
- operadores lógicos:
| símbolo | nombre | se lee como |
| ʌ | conjunción lógica | y |
| v | disjunción lógica | o |
| ¬ | negación lógica | no |
| ⇒ | implicación en sentido único | entonces |
| ⇔ | doble implicación | si y solo si |
- operadores de conjuntos:
| símbolo | nombre | se lee como |
| {,} | delimitadores de conjuntos | el conjunto formado por |
| ∈ | pertenencia a conjuntos | pertenece a |
| ∉ | pertenencia a conjuntos (negación) | no pertenece a |
| ∪ | unión de conjuntos | la unión de ... y ... |
| ∩ | intersección de conjuntos | la intersección de ... y ... |
- cuantificadores:
| símbolo | nombre | se lee como |
| ∀ | cuantificador universal | para cualquier |
| ∃ | cuantificador existencial | existe como mínimo |
| ∄ | cuantificador existencial (negación) | no existe ningún |
| : | tal que |
- números:
| símbolo | nombre | se lee como |
| N | números naturales | N |
| Z | números enteros | Z |
| Q | números racionales | Q |
| R | números reales | R |
| C | números complejos | C |
| √ | raíz cuadrada | raíz de |
| ∞ | infinito | infinito |
| | | | valor absoluto | valor absoluto de |
| % | porcentaje | porcentaje de |
A continuación hacemos una breve explicación de los cuantificadores, su significado y su utilización:
Cuantificador universal
El cuantificador universal, escrito ∀, se utiliza para indicar que todos los elementos de un conjunto cumplen una condición.
Ejemplo 02_02: si queremos decir que para todo número real su cuadrado también es real, escribimos:
∀x ∈ R ⇒ x*x ∈ R
Recordad que el símbolo ∈ se lee como "pertenece a". Por lo tanto, el predicado anterior se lee de la siguiente manera: para todo (∀) x que pertenezca a los reales, su cuadrado también pertenece a los reales.
Ejemplo 02_03: si queremos decir que dados dos números reales menores que 1 su producto es otro nombre real menor que 1 escribimos:
∀x,y ∈ R: x<1 ʌ y<1 ⇒ x*y < 1
Cuantificador existencial:
El cuantificador existencial, escrito (∃) indica que al menos hay un elemento de un conjunto dado que cumple una condición.
Ejemplo 02_04: si queremos decir que dado un número real x positivo existe otro que es su raíz cuadrada, escribimos:
∀x ∈ R, ∃y ∈ R: x>0 ⇒ y*y = x
Muchas veces los cuantificadores se combinan en un mismo predicado. Veamos un ejemplo:
Ejemplo 02_05: si queremos decir que entre dos números reales siempre hay otro real, escribimos:
∀x,z ∈ R, ∃y ∈ R: x<z ⇒ x<y<z
Ejemplo 02_06: predicados con cuantificadores aplicados a la especificación :
Supongamos que queremos escribir la especificación de un método que calcule el máximo común divisor de dos enteros. Cómo lo escribiríamos formalmente?
Variables: necesitamos dos variables para indicar que se espera a la entrada del método. Estas variables pueden ser parámetros del método. Además, necesitamos otra variable para guardar el resultado. La definición sería:
var
x, y, mcd: interger;
end var
Precondición: debemos indicar que el método recibe dos enteros positivos. Cómo lo hacemos? Escribimos:
{ Pre: x=X ʌ y=Y ʌ X>0 ʌ Y>0 }
Hemos dicho que el método debe recibir dos enteros cualesquiera positivos (no sabemos sus valores, pero los valores que recibirán los indicamos con X e Y.)
Nombre del algoritmo: en este caso podemos llamarle maxComunDivisor.
Postcondición: debemos indicar que la variable mcd debe de ser un divisor de X e Y, y además no puede haber ningún otro entero mayor que mcd que cumpla la condición de ser divisor de X e Y. Lo escribimos de la siguiente manera:
{ Post: X mod mcd = 0 ʌ Y mod mcd = 0 ʌ ∀j ∈ N: j>mcd ʌ (X mod j ≠ 0 v Y mod j ≠ 0) }
En la postcondición decimos que la variable mcd es divisor de X y de Y y que cualquier entero mayor que mcd o no es divisor de X o no lo es de Y.
Especificación y programación
Aunque las precondiciones sirven para indicar cuales son los valores de entrada válidos para un algoritmo o método, y es responsabilidad del que ejecuta el algoritmo entrar datos con los valores adecuados, siempre es aconsejable antes de ejecutar un algoritmo o método, comprobar que se cumple la precondición. Si se detecta que la precondición no se cumple debe darse un error y parar la ejecución del programa.
Supongamos que debemos escribir una función con la especificación de uno de los ejemplos anteriores. Es decir una función que, dado un entero positivo number, devuelva la suma de los cuadrados de 1 hasta number. Se debería poner una comprobación de que el parámetro actual pasado en la llamada a la función no sea negativo. Si es negativo se para la ejecución del programa.
En C hay una función que permite comprobar el valor de una variable y en caso de que no cumpla la condición el programa se para. Es la macro assert. Para utilizarla hay que incluir la librería assert.h.
#include <assert.h>
Para comprobar que la variable number es mayor que 0 debemos escribir en el código:
assert(number > 0);
Si number tiene un valor negativo o 0, el programa se parará.
El siguiente ejemplo muestra como se escribiría:
[Ejemplo 02_07]
function squareAddition (number: integer): integer
var sum: integer;
{ Pre: number = NUMBER ʌ NUMBER >0 }
if (number ≤ 0) then
stop program
{ Post: sum = ∑+(i=1)^NUMBER (i^2) }
{ ... }
end function
#include <assert.h>
int squareAddition(int number) {
int sum;
/* { Pre: number = NUMBER ʌ NUMBER >0 } */
assert(number > 0)
/* { Post: sum = ∑+(i=1)^NUMBER (i^2) } */
/* ... */
}
Las aserciones normalmente se pueden activar o desactivar. En C, para desactivarlas se debe incluir la directiva #define NDEBUG al inicio del programa. Esta directiva desactiva las aserciones incluidas en el programa. De esta manera se pueden incluir asserts en el programa mientras se está desarrollando y se pueden desactivar cuando el programa ya está probado.
Ejemplo 02_08
Problema: especificar un método que, dado un importe en euros, se pueda obtener con billetes mayores o iguales a 20€ calcule el mínimo número de billetes de cada tipo necesarios para obtener el importe dado.
Por ejemplo, si tenemos el importe 2.370€ el resultado esperado sería:
4 billetes de 500€ 2.000
1 billete de 200€ 200
1 billete de 100€ 100
1 billete de 50€ 50
1 billete de 20€ 20
Total 2.370
Y si tenemos el importe 420€, el resultado sería:
2 billetes de 200€ 400
1 billete de 20€ 20
Total 420
Especifiquemos el método paso a paso
Variables: lo primero que tenemos que hacer es especificar las variables que vamos a necesitar. En este caso necesitaremos una variable de tipo entero para representar el importe de entrada.
Pensemos ahora en qué variables necesitamos para la salida. Como tenemos que desglosar el importe en billetes, necesitaremos al menos una variable para cada tipo de billete. Por lo tanto necesitaremos lo siguiente:
var
quantity: integer;
fiveHundred: integer;
twoHundred: integer;
oneHundred: integer;
fifties: integer;
twenties: integer;
end var
int quantity;
unsigned short fiveHundred;
unsigned short twoHundred;
unsigned short oneHundred;
unsigned short fifties;
unsigned short twenties;
Precondición: para escribir la precondición debemos pensar en qué debe cumplirse respecto a la variable de entrada, en este caso quantity. Tiene que ser positiva y debe ser múltiplo de 20 o de 50, ya que no podemos utilizar billetes de 10. Por lo tanto escribimos:
{ Pre: quantity=QUANTITY ʌ QUANTITY>0 ʌ (QUANTITY mod 20 = 0 v QUANTITY mod 50 = 0) }
Es decir, decimos que el valor inicial de quantity está representado por QUANTITY y que éste debe de ser positivo y múltiplo de 20 o de 50; dicha condición la validamos mediante el operador mod. Con esta precondición, el importe 110 no sería aceptable, ni tampoco lo sería 20.010, ya que ambos valores no son múltiplos de 20 ni de 50.
Nombre del algoritmo: podemos escoger el nombre que nos guste. Podríamos llamarle por ejemplo divideQuantity.
Postcondición: en la postcondición debemos decir como deben ser les variables de salida. Lo primero que podemos decir es que la suma de los billetes debe ser igual al importe inicial. Tendríamos:
{ Post: QUANTITY = 500*fiveHundred + 200*twoHundred + 100*oneHundred + 50*fifties + 20*twenties }
Ahora bien, es suficiente lo que hemos escrito? Es fácil ver que la postcondición que hemos escrito cumple con el hecho de que cantidad final sería correcta, pero no cumple necesariamente la condición de que se utilice el mínimo número de billetes. Por ejemplo, 420 lo podríamos representar con 21 billetes de 20, pero no sería la solución que se busca.
Por lo tanto la postcondición debe ser más restrictiva. Para hacerlo debemos pensar en cuál es el número máximo de billetes que podemos usar de cada tipo:
- De 500 podemos usar cualquier número
- De 200 solamente podemos usar 2 para sumar hasta 400, ya que 3 sumarían 600 que se puede representar con uno de 500 y uno de 100.
- De 100 solamente podemos usar 1.
- De 50 solamente podemos usar 1.
- De 20 podemos usar hasta 4.
Por lo tanto, la postcondición completa será:
{ Post: (QUANTITY = 500*fiveHundred + 200*twoHundred + 100*oneHundred + 50*fifties + 20*twenties) ʌ
(0 ≤ fiveHundred) ʌ (0 ≤ twoHundred ≤ 2) ʌ (0 ≤ oneHundred ≤ 1) ʌ (0 ≤ fifties ≤ 1) ʌ (0 ≤ twenties ≤ 4) }
Resumen
En esta unidad hemos visto como especificar un problema de manera formal.
- Se han definido los elementos de la especificación.
- Se han introducido los elementos básicos del cálculo de predicados que nos permite escribir la especificación de una manera formal.
- Se ha visto un ejemplo en detalle explicando paso a paso como definir la precondición y la postcondición.