Introducción

Como ya se ha comentado en el módulo Introducción a la Complejidad es necesario establecer un criterio para decidir entre varios algoritmos que resuelven un mismo problema.

Con éste objetivo analizamos la eficiencia de un algoritmo en base a su tiempo de ejecución. El tiempo de ejecución de un algoritmo nos determina su complejidad, es decir la velocidad de crecimiento del tiempo de ejecución al aumentar el tamaño de la entrada.

En éste módulo analizaremos cómo calcular el tiempo de ejecución de un algoritmo con el objetivo de determinar su complejidad.

Repaso notación asintótica

En el módulo de Introducción a la Complejidad se ha comentado que la eficiencia de un algoritmo depende de su tiempo de ejecución, T( n ). A este tiempo se le puede describir con una función f( n ), que nos indica que T( n ) es proporcional a f( n ). Se comentó también que la notación asintótica nos sirve para indicar la velocidad de crecimiento de una función del tiempo de ejecución de un algoritmo. Decimos que T( n ) es O(f( n )) cuando la velocidad de crecimiento de T( n ) está acotada superiormente por f( n ). Así O(f( n )) representa el conjunto de todas las funciones g( n ) que crecen como mucho tan rápidamente como f( n ).

Ejemplo 10_01 : el conjunto de funciones O(20n³) es lo mismo que O(n³)

Solución : a partir de la definición de O( f ) queda claro que las constantes no tienen ningún efecto en la notación asintótica, y por lo tanto pueden ser ignoradas. En este caso si la constante c = 20, tenemos que toda función que está dentro de O(20n³) también está dentro de O(n³).

Ejemplo 10_02 : el conjunto de funciones O(20n³ + 40n² + 80n) es lo mismo que O(n³)

Solución : según la definición asintótica, añadir términos a f con una velocidad de crecimiento menor no afecta al conjunto de funciones que forma parte de O(f( n )). Es decir que si g( n ) ∈ O(f( n )) entonces O( f( n ) + g( n ) ) = O( f( n ) ).

Ejemplo 10_03 : Regla de la suma: P₁ y P₂ dos algoritmos con tiempos de ejecución T₁( n ) y T₂( n ) respectivamente, que son O(f( n )) y O(g( n )). Si P₁ y P₂ se ejecutan secuencialmente, entonces la complejidad de su composición es O(max(f( n ), g( n ))).

Solución : el tiempo de ejecución corresponderá a la suma de ambos tiempos (son secuenciales), por lo tanto es T₁( n ) + T₂( n ), que tendrá complejidad O(max(f( n ), g( n ))). Esto último viene del hecho de que corresponde a la velocidad de crecimiento mayor según se ha visto en un caso de estudio anterior.

Ejemplo 10_04 : Regla del producto: P₁ y P₂ dos algoritmos con tiempos de ejecución T₁( n ) y T₂( n ) respectivamente, son O(f( n )) y O(g( n )).

Solución : el tiempo resultado del producto T₁( n ).T₂( n ) tiene complejidad igual a la complejidad del producto de las funciones: O(f( n ) . g( n )).

Ejemplo 10_05 : de las reglas del producto y la suma se deriva:

• Dado T( n ) = c  entonces T( n ) = O(1).
• Dado T( n ) = c + f( n ) entonces T( n ) = O(f( n )).
• Dado T( n ) = c . f( n ) entonces T( n ) = O(f( n )).

Análisis de algoritmos

Cuando se analiza un algoritmo lo que se hace es analizar la complejidad de cada una de sus partes, y luego calcular la complejidad resultado de su composición. En general los algoritmos suelen estar compuestos por partes secuenciales y partes iterativas.

A continuación veremos la complejidad para los tipos de sentencias más habituales de un algoritmo.

Asignación

La asignación tiene tiempo constante por lo tanto tiene orden de complejidad O(1).

Ejemplo 10_06 :

    a := 100;
    a := a + 1;
    a := (b div 4) mod 8 + 1000;

Secuencia de instrucciones

Dada la secuencia de instrucciones: P₁;P₂;..;P_k con T_i( n ) = O(f_i( n )) respectivamente, la complejidad de la secuencia está dada por la expresión:

        k

    ∑ T_i ( n ) = O(max{f₁( n ), f₂( n ), .., f_k( n )})

    i = 1

Sentencia condicional

Dada la siguiente forma de sentencia condicional:

if <condicion> then <instrucciones> end if

El tiempo de ejecución de esta sentencia está dado por el tiempo de <condición> que denominamos T₁( n ), sumado al tiempo de <instrucciones> (sería el peor caso) que denominamos T₂( n ). Por la regla de la suma, si T₁( n ) tiene orden de complejidad O(f( n )) y T₂( n ) tiene orden de complejidad O(g( n )), entonces el tiempo de la sentencia condicional es T₁( n ) + T₂( n ) y el orden de complejidad es O(max{f( n ),g( n )}.

Para una sentencia condicional de la forma:

if <condicion> then <instrucciones1> else <instrucciones2> end if

El tiempo de ejecución de esta sentencia está dado por el tiempo de <condición> que denominamos T₁( n ), sumado al máximo de los tiempos de ejecución (sería el peor caso) de <instrucciones1> e <instrucciones2> que denominamos T₂( n ) y T₃( n ) respectivamente.  Si consideramos que O(f( n )), O(g( n ))  y O(h( n )) son los órdenes de complejidad de T₁( n ), T₂( n ) y T₃( n ) respectivamente, la complejidad de la expresión T₁( n ) + max{T₂( n ),T₃( n )},  por la regla de la suma, está dada por O(max{f( n ), max{g( n ), h( n )}}, o sino más sencillamente O(max{f( n ), g( n ), h( n )}).

Ejemplo 10_07 :

Dado el siguiente trozo de código:

1    if (a > 0) then

2            b := a;

3    else

4      b := a + b - 48*(a%1003);

5        end if

Calcular el tiempo de ejecución y su complejidad.

El tiempo de ejecución es T( n ) = T₁( n ) + max{T₂( n ), T₄( n )}, siendo T₁, T₂ y T₄ los tiempos de ejecución de las líneas 1, 2 y 4 respectivamente. Dado que la comparación y la asignación tienen complejidad constante, tenemos que:

T( n ) = k₁ + max{k₂, k₄} = k, por lo tanto el orden de complejidad es constante (O(1)).

Sentencia iterativa

El tiempo de ejecución de una sentencia iterativa que ejecuta k iteraciones, está dado por el tiempo de evaluar la condición k + 1 veces sumado al tiempo de ejecutar k iteraciones.

Para una sentencia iterativa de la forma:

while <condicion> do <instrucciones> end while

El tiempo de ejecución de esta sentencia está dado por el tiempo de <condición> que denominamos T₁( n ), sumado al tiempo del bucle. Si <instrucciones> con tiempo de ejecución T₂( n ) se ejecutan k veces, tenemos que <condición> se ejecuta k + 1 veces por lo que el tiempo de ejecución total viene dado por la expresión:

                                    k

  T( n ) = T₁( n ) + ∑ (T₁( n ) + T₂ ( n )) = T₁( n ) + k .(T₁( n ) + T₂( n ))

                                i=1

Ejemplo:

Dado el siguiente trozo de código calcular el tiempo de ejecución y su complejidad:

1      i := 1;

2            count := 0;

3      while (i ≤ n) do

4            if (v[i] = x) then

5                 count := count + 1;

6            end if

7            i := i + 1;

8      end while

En una secuencia de instrucciones, el tiempo total está dado por la suma de los tiempos de cada instrucción. Si T₁( n ) y T₂( n ) corresponden al tiempo de ejecución de las líneas 1 y 2 respectivamente, y T_3-8( n ) al tiempo de ejecución del bucle, el tiempo total está dado por la expresión:

T( n ) = T₁( n ) + T₂( n ) + T_3-8( n )

Las asignaciones tienen tiempo constante, por lo que T₁( n ) = k₁  y T₂( n ) = k₂

El tiempo de ejecución de las instrucciones del bucle:

El tiempo de una sentencia condicional está dado por el tiempo de la condición T₄( n ) (línea 4) sumado al tiempo de las instrucciones de la sentencia condicional (peor caso), T₅( n ).

Si T₃( n ) es el tiempo de evaluar la condición del bucle (línea 3), T₇( n ) es el tiempo de la línea 7, tenemos que el tiempo de las instrucciones del bucle está dado por la expresión: T₃( n ) + T₄( n ) + T₅( n ) + T₇( n ).

Por lo tanto, si el número de iteraciones totales es n, tenemos que:

T_3-8( n ) = T₃( n ) + n . (T₃( n ) + T₄( n ) +  T₅( n ) + T₇( n ))

Dado que las asignaciones y comparaciones tienen tiempos constantes:

  T_3-8( n ) =  k₃ + n. (k₃ + k₄ + k₅ + k₇)

El tiempo total del trozo de código del ejemplo es:

T( n ) = k₁ + k₂ + k₃ + n. (k₃ + k₄ + k₅ + k₇) = k + n . k  y esto tiene complejidad lineal O( n ).

Análisis de recurrencia

Para realizar el análisis de algoritmos recursivos se procede igual que con los algoritmos no recursivos: se calcula primero su función del tiempo de ejecución y luego se expresa ésta en notación asintótica.

La definición del tiempo de ejecución T( n ) de un algoritmo recursivo está en función de los tiempos de ejecución de cada invocación recursiva, es decir de sí misma, por lo que ésta función es recurrente.

La resolución de ecuaciones recurrentes, puede ser bastante compleja. Un método para resolver éste tipo de ejecuaciones consiste en aplicar la definición recurrente en forma repetida hasta que se pueda aplicar el caso base, es decir la parte no recurrente de la definición.

Ejemplo 10_09 :

Resolver la ecuación siguiente (ejemplo extraído de [1]):

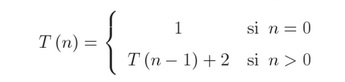
Resolver dicha ecuación significa obtener una expresión para T( n ) que no esté en función de sí misma sino de n.

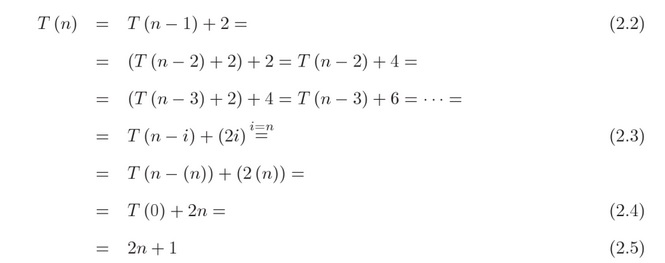
El método consiste en rescribir la definición recursiva (2.2) y a continuación sustituir T( n-1 ) por la definición recursiva, pero en función ahora de n-1. Este paso se repite varias veces hasta hacerlo genérico para i veces (2.3). Llegado este punto es necesario averigual que valor tiene que tener i de forma de convertir la expresión genérica en el caso base. En este ejemplo, el  caso base sucede cuando n = 0, por lo tanto para convertir el caso genérico en el caso base, tiene que ser i = n. De esta forma llegamos primero a (2.4) y dado que T( 0 ) = 1 por definición de la función, llegamos a (2.5). Por lo tanto, la resolución de T( n ) es T( n ) = 2n + 1.

Ejemplo 10_10 :

Calcular la complejidad computacional de la acción replace.

Para analizar la complejidad computacional de esta acción, hay que observar que en cada llamada el valor del parámetro size disminuye en una unidad y cuando llega a 0 entonces finaliza la recursividad. Por lo tanto, la función de tiempo hay que definirla en función de n = size.

Así pues, podemos definir la función de tiempo de la siguiente manera:

Resolvemos la recurrencia repitiendo la sustitución recursiva un total de i veces:

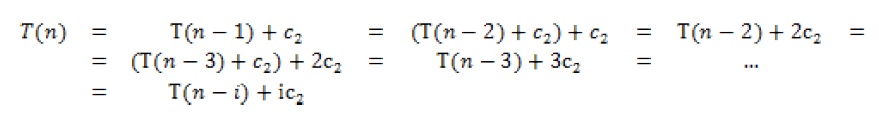
Calculamos el valor de la variable i que hace que se pueda aplicar la parte no recurrente de la definición de T( n ) :

n - i = 0
n = i

Finalizamos el cálculo de T( n ) con el valor calculado para la variable i:

La conclusión es que la acción replace tiene complejidad lineal O( n ), donde n es el valor del parámetro size.

Ejemplo 10_11 :

Calcular la complejidad computacional de la función sumCount. Se puede asumir que el número máximo de elementos de la lista de cada entrada de la tabla coincide con el tamaño de vector (N). Se sabe que la función de tiempo de countNeg es T_c( n ) = k₁ + n·k₂ que tiene complejidad computacional lineal (O( n )), siendo n el número de elementos de la lista en el peor caso.

Para analizar la complejidad de sumCount es necesario plantear su función de tiempo, la cual calcularemos en función del tamaño del vector de entrada, m y que denominaremos T_s( m ). Consideraremos el peor caso que es cuando el número de elementos (nelem) es igual a m. Por lo tanto la función de tiempo de sumCount se puede plantear como sigue:

     T_s( m ) = k₃ , si m = 0
    T_s( m ) = k₄ + T_c( n ) + T_s( m-1 ) , si m > 0

El caso base consta de una comparación y una asignación. Dado que ambas son operaciones elementales tiene un costo de tiempo constante que llamaremos k₃.

El caso recursivo consta de una asignación y una suma con tiempo constante k₄, una invocación a la función countNeg con tiempo dado por la función T_c y una invocación recursiva a sumCount. Por lo tanto la función de tiempo para calcular el costo de la llamada recursiva es:

   T_s( m ) = k₄ + T_c( n ) + T_s( m-1 ) = k₄ + T_c( n ) + (k₄ + T_c( n ) + T_s( m-1-1 )) =
              = k₄ + k₄ + T_c( n ) + T_c( n ) + T_s( m-1-1 ) = 2k₄ + 2T_c( n ) + T_s( m-2 ) =
              = 2k₄ + 2T_c( n ) + (k₄ + T_c( n ) +T_s( m-2-1 )) = 3k₄ + 3T_c( n ) + T_s( m-3 ) =
              = … =
              = i·k₄ + i·T_c( n ) + T_s( m-i )

Para poder aplicar el caso base, m debe ser igual a i, ya que queremos T_s( 0 ). Completamos el cálculo con i = m y aplicamos el caso base:

   T_s( m ) = m·k₄ + m·T_c( n ) + T_s( m-m ) = m·k₄ + m· T_c( n ) + T( 0 ) =
                = m·k₄ + m·T_c( n ) + k₃

Dado que el número elementos de la función de tiempo T_c( n ) en el peor caso coincide con el tamaño de la tabla, podemos utilizar n en lugar de m. Por lo tanto, podemos reescribir la función de tiempo T_s( n ) de sumCount como:

T_s( n ) = n·k₄ + n·(k₁ + n·k₂) + k₃ = k₃ + n·(k₁ + k₄) + n² ·k₂ = O(n²)

Podemos decir que la función sumCount tiene una complejidad cuadrática, O(n²), siendo n el número de elementos en el vector de entrada.

Resumen

En éste módulo se ha repasado la notación asintótica y se han dado los conceptos básicos para el análisis de algoritmos. Se ha introducido el cálculo de la función de tiempo para tipos de sentencias comunes como: asignación, sentencia condicional, sentencia iterativa. Y se ha calculado a partir de la función de tiempo su complejidad.

Por último se ha visto análisis de algoritmos recurrentes y un método para calcular su función de tiempo.

Bibliografía

[1] Manual de Algorítmica: Recursividad, complejidad y diseño de algoritmos. Jesús Bisbal Riera