08. Tipos de datos: vectores y matrices
Objetivos
- Entender el concepto de vector y matriz.
- Indexación en vectores y matrices.
- Representación a memoria de lo vectores y las matrices.
Introducción
Hasta ahora hemos visto que las variables son objetos que pueden contener valores de diferentes tipos, como por ejemplo, enteros, reales o caracteres. En esta unidad veremos que podemos definir variables que contienen varios elementos de un mismo tipo. Según estas variables tengan 1 o 2 dimensiones, las llamaremos vectores o matrices respectivamente. También veremos cómo podemos acceder a cada uno de los elementos de un vector o de una matriz, y cómo estos quedan almacenados en memoria.
1. Vectores
Los vectores, o arrays en inglés, son estructuras de una sola dimensión, que pueden almacenar n valores de un mismo tipo. Por ejemplo, imagina que queremos guardar las temperaturas máximas de cada día de la semana. Con lo que hemos visto hasta ahora, tendríamos que definir 7 variables, una para cada día:
var
t1, t2, t3, t4, t5, t6, t7: real;
end var
float t1,t2,t3,t4,t5,t6,t7;
Si lo definimos en forma de vector, podemos crear un objeto que pueda guardar los 7 valores:
var
t : vector[7] of real;
end var
float t[7];
Para acceder a la enésima posición de un vector lo haremos con [n] donde n es la posición a la que queremos acceder, por ejemplo, t[3]. Un punto muy importante a tener en cuenta cuando trabajamos con vectores es qué valor tiene la primera posición. En algunos lenguajes, la primera posición tiene un valor 0, por lo tanto, t[0] sería la primera temperatura, mientras que en otros lenguajes, se considera que la primera posición tiene valor 1 y, por tanto, para obtener la primera temperatura deberíamos escribir t[1]. Cuando trabajamos con lenguaje algorítmico utilizamos como primera posición la 1, ya que en notación matemática, la primera posición de un vector es ésta. Cuando trabajamos con lenguaje C, la primera posición será siempre 0.
Por tanto, la expresión para calcular la temperatura media sería:
(t[1] + t[2] + t[3] + t[4] + t[5] + t[6] + t[7]) / 7;
Si lo ponemos todo junto en un algoritmo que nos pida las temperaturas y nos muestre la temperatura media, tendremos el siguiente:
[Ejemplo 08_01]
algorithm meanTemp
var
t: vector[7] of real;
m: real;
end var
t[1] := readReal();
t[2] := readReal();
t[3] := readReal();
t[4] := readReal();
t[5] := readReal();
t[6] := readReal();
t[7] := readReal();
m:=(t[1] + t[2] + t[3] + t[4] + t[5] + t[6] + t[7]) /7;
writeReal(m);
end algorithm
int main(int argc, char** argv) {
float t[7];
float m;
scanf("%f %f %f %f %f %f %f", &(t[0]), &(t[1]), &(t[2]), &(t[3]), &(t[4]), &(t[5]), &(t[6]));
m=(t[0] + t[1] + t[2] + t[3] + t[4] + t[5] + t[6]) /7;
printf("%f", m);
return 0;
}
Dado que cuando se carga un programa para su ejecución se reserva la memoria para sus variables y entre ellas los vectores, cuando definimos un vector podemos utilizar constantes para su dimensión, pero nunca variables, ya que estas no tienen un valor conocido hasta que ya se está ejecutando el programa. Por tanto, podemos hacer:
#define N 3
int main(int argc, char** argv) {
float v[N];
}
y no podemos hacer:
int main(int argc, char** argv) {
int m=3;
float v[m];
}
Cuando la longitud de un vector es un dato del problema, es una buena práctica definirla como una constante, ya que nos permite modificar este dato rápidamente. Por ejemplo, si en el caso de las temperaturas semanales, quisiéramos cambiar para que fuesen anuales, habría que cambiar el número de posiciones 7 por 365, y en el cálculo de la media también habría que dividir por 365 en vez de 7. Si lo tuviéramos definido a partir de una constante, solo habría que cambiar la constante.
1.1. Cadenas de caracteres o strings
Un tipo muy utilizado de vector son las cadenas de caracteres, a menudo conocidas por su nombre en inglés strings. En C, para definir una cadena de caracteres lo haremos como un vector normal, pero hay que tener en cuenta que las cadenas de caracteres, para poder ser interpretadas como tales, deben finalizar siempre con el carácter ('\0'), que tiene valor ASCII 0. Por lo tanto, si queremos guardar una cadena de caracteres será necesario reservar memoria para una posición adicional.
En lenguaje algorítmico generalmente no se declara como vector sino como cadena de caracteres. A continuación se muestra un ejemplo:
[Ejemplo 08_02]
algorithm sayHello
var
name: string;
end var
writeString("What's your name?");
name := readString();
writeString("Hello" + name);
end algorithm
#define MAX_NAME_LEN 25
int main(int argc, char** argv) {
char name[MAX_NAME_LEN];
printf("What's your name?\n");
scanf("%s", name);
printf("Hello %s\n", name);
return 0;
}
Fijaos en que en el caso de las cadenas de caracteres, cuando utilizamos la instrucción en C scanf no ponemos el símbolo & delante.
1.2. Representación en memoria
Todas las posiciones de un vector se guardan en memoria consecutivamente y, por tanto, un vector de n posiciones ocupará n veces lo que ocupa su tipo básico. Por ejemplo, si tenemos un vector de enteros a, y un entero ocupa 4 bytes en memoria de manera que ocupa hasta la posición X, el vector de 4 enteros ocupará 4x4 = 16 bytes en memoria:

La representación gráfica de cómo queda en memoria una variable es una herramienta muy útil para hacer el seguimiento del programa. Con este fin, podemos poner en orden inverso las posiciones, suponer que la posición inicial es 0 y agrupar los bytes que contienen un valor del vector. Por ejemplo, si el vector contiene los valores {1, 4, -1, 1023}, lo podemos representar como:

1.3. Incicialización
Al igual que una variable de tipo básico, los vectores también se pueden inicializar cuando los definimos. En este caso utilizaremos las llaves ({ y }) para indicar que es un vector. Cuando inicializamos un vector, no es obligatorio definir su longitud, ya que se obtiene a partir del número de elementos dados. Por ejemplo:
[Ejemplo 08_03]
var
v1 : vector[3] of integer:={3, 5, -1} ;
v2 : vector of integer:={3, 5, -1} ;
v2 : vector[4] of integer:={3, 5, -1} ;
end var
/* Variable definition*/
int v1[3] = {3, 5, -1};
int v2[] = {3, 5, -1};
int v3[4] = {3, 5, -1};
En C, tened en cuenta que v2 no tiene especificada la longitud, y por tanto se definirá como un vector de enteros con 3 posiciones. En el caso de v3, es un vector de 4 posiciones del que solo inicializamos las 3 primeras.
En el caso de las cadenas de caracteres, podemos utilizar las comillas dobles ("), o tratarlo igual que un vector normal y asignar carácter a carácter. A continuación se muestra un ejemplo de código donde se inicializan las cadenas de caracteres de diferentes formas y se muestra para cada variable su contenido y el tamaño en bytes. Tened en cuenta que cuando utilizamos las comillas dobles se añade el símbolo de final de cadena ('\0') automáticamente.
[Ejemplo 08_04]
int main() {
char a[] = {'a','b','c','\0'};
char b[4] = {'a','b','c','\0'};
char c[] = "abc";
char d[4] = "abc";
printf("a - %s --> (%d) bytes\n", a, sizeof(a));
printf("b - %s --> (%d) bytes\n", b, sizeof(b));
printf("c - %s --> (%d) bytes\n", c, sizeof(c));
printf("d - %s --> (%d) bytes\n", d, sizeof(d));
return 0;
}
2. Matrices
Las matrices son vectores de dos dimensiones. Por ejemplo, para definir la matriz:
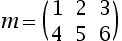
Lo podemos hacer de la siguiente forma:
var
m : matrix[2][3] of integer:={{1, 2, 3}, {4, 5, 6}} ;
end var
int m[2][3] = {{1, 2, 3}, {4, 5, 6}};
Tened en cuenta que primero se declara el número de filas y luego el de columnas. Al igual que en el caso de los vectores, hay que tener en cuenta que los índices de las posiciones pueden empezar en 0 o en 1. A continuación se muestra un ejemplo en el que se calcula el valor promedio de todos los valores de la matriz anterior.
[Ejemplo 08_05]
algorithm matMean
var
m : matrix[2][3] of integer:={{1, 2, 3}, {4, 5, 6}} ;
r : real;
end var
r:=integerToReal(m[1][1] + m[1][2] + m[1][3] + m[2][1] + m[2][2] + m[2][3]);
r:= r/6;
writeReal(r);
end algorithm
int main() {
/* Variable definition*/
int m[2][3] = {{1, 2, 3}, {4, 5, 6}};
float r;
r=(m[0][0] + m[0][1] + m[0][2] + m[1][0] + m[1][1] + m[1][2])/6.0;
printf("%f\n", r);
return 0;
}
Cuando se guarda en memoria, se hace por filas. Por tanto, una matriz como la anterior en memoria es equivalente a un vector de 2x3 = 6 posiciones y por tanto de 6x4 = 24 bytes.

3. Ejemplos
3.1. Ejemplo 08_06
Definir un algoritmo que calcule el producto escalar de dos vectores en un espacio de dos dimensiones (2D).
algorithm dotProduct
var
a : vector[2] of integer;
b : vector[2] of integer;
c : integer;
end var
a[1] := readInteger();
a[2] := readInteger();
b[1] := readInteger();
b[2] := readInteger();
c:= a[1] * b[1] + a[2] * b[2];
writeInteger(c);
end algorithm
int main() {
/* Variable definition*/
int a[2], b[2];
int c;
scanf("%d %d %d,%d", &(a[0]), &(a[1]), &(b[0]), &(b[1]));
c=a[0] * b[0] + a[1] * b[1];
printf("(%d,%d) * (%d,%d) = %d\n", a[0], a[1], b[0], b[1], c);
return 0;
}
3.2. Ejemplo 08_07
Definir un algoritmo que calcule el producto entre la matriz identidad de 3x3 y un valor entero introducido por teclado.
algorithm dotProduct
var
id : matrix[3][3] of integer := {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
s : integer;
r : matrix[3][3] of integer;
end var
s := readInteger();
r[1][1]:= id[1][1] * s;
r[1][2]:= id[1][2] * s;
r[1][3]:= id[1][3] * s;
r[2][1]:= id[2][1] * s;
r[2][2]:= id[2][2] * s;
r[2][3]:= id[2][3] * s;
r[3][1]:= id[3][1] * s;
r[3][2]:= id[3][2] * s;
r[3][3]:= id[3][3] * s;
end algorithm
int main() {
/* Variable definition*/
int id[3][3]={{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
int s;
int r[3][3];
scanf("%d", &s);
r[0][0] = id[0][0] * s;
r[0][1] = id[0][1] * s;
r[0][2] = id[0][2] * s;
r[1][0] = id[1][0] * s;
r[1][1] = id[1][1] * s;
r[1][2] = id[1][2] * s;
r[2][0] = id[2][0] * s;
r[2][1] = id[2][1] * s;
r[2][2] = id[2][2] * s;
return 0;
}
Resumen
En esta unidad hemos visto cómo definir e inicializar vectores y matrices, tanto en lenguaje algorítmico como en los lenguajes de programación. También hemos visto cómo acceder a los valores de un vector y matriz tanto para utilizarlos, como para asignar nuevos valores. Además hemos visto que las cadenas de carácter son un vector con algunas propiedades a tener en cuenta cuando programamos en lenguaje C.