19. Tipos abstractos de datos
Objetivos
- Entender el concepto de tipo abstracto de datos (TAD). Qué significa y cuál es su utilidad.
- Entender los TADs que representan secuencias de elementos. En particular se estudian: pilas, colas y listas.
Introducción
En esta unidad se presenta el concepto de tipo abstracto de datos (TAD). En particular se introducen los TADs para representar secuencias de elementos tales como: lista, cola y pila. La diferencia entre estos tipos de secuencias viene dada por el tipo de operaciones que les podemos aplicar, las cuales definen su comportamiento. Los TADs que se presentan en esta unidad emulan conceptos que encontramos fuera del mundo de la programación.
Ejemplos de listas pueden ser la lista de la compra, el listado de estudiantes de una clase o la guía telefónica. Todos estos ejemplos tienen en común que contienen una secuencia de elementos (cosas a comprar, nombres de personas o teléfonos) y que en cualquier momento podemos ver y modificar cualquiera de los elementos y en cualquier orden. Por ejemplo, si vamos a comprar con una lista de la compra, iremos tachando los productos que ya hemos comprado en el orden que los compramos, no en el orden en que aparecen en la lista.
Ejemplos de colas también encontramos a nuestro alrededor. Por ejemplo, en la entrada de un concierto o en la parada del autobús. Ambos ejemplos constan de un conjunto de personas una tras otra (secuencia). En este caso, sin embargo, el comportamiento es diferente. Entendemos que cuando llegue una nueva persona se pondrá siempre detrás de la cola y que la primera persona en salir de la cola (para entrar en el concierto o en el autobús) será la primera que ha llegado, o sea, la que está delante. Este comportamiento conocido como FIFO (First In First Out) es lo que define una cola.
Finalmente, también estamos acostumbrados a tener pilas a nuestro alrededor. Por ejemplo, sobre el escritorio, donde vamos acumulando los apuntes de la universidad, o una pila de platos en el armario. En ambos casos, volvemos a tener un conjunto de objetos (hojas de apuntes o platos) y, en este caso, el comportamiento es diferente. Cuando tenemos una pila de objetos, el objeto que lleva más tiempo en la pila es el de abajo del todo y para llegar a él hay que sacar todo lo que tiene encima. Por lo tanto, si quiero coger un plato de una pila de platos, tendré que coger el que se encuentra en la parte superior, o sea, el último que he dejado en la pila. Este comportamiento conocido como LIFO (Last In First Out) es lo que define una pila.
En esta unidad veremos cómo definir estructuras de datos que emulan estos comportamientos y qué operaciones nos permitirán añadir, acceder y eliminar los elementos que se encuentran en ellas. Hay que tener presente que no veremos ningún tipo de dato nuevo, solo cómo podemos utilizar los que ya hemos visto anteriormente para emular estos comportamientos.
1. Tipo abstracto de datos (TAD)
Un TAD consiste en un conjunto de valores (dominio) y el conjunto de operaciones que se pueden aplicar a este conjunto de valores.
El concepto de tipo abstracto de datos es necesario para poder modelar y representar un objeto mediante un tipo de datos de la forma más descriptiva, con todas las características que lo definan.
El concepto de TAD ya existe en los lenguajes de programación bajo la forma de tipos predefinidos. Por ejemplo, en C, el tipo de datos int tiene como dominio todos los enteros en el rango [MININT, MAXINT] y las operaciones que se le aplican son: suma, resta, producto, cociente y módulo.
Se agrega la palabra «abstracto» a tipo de datos, para indicar que la definición del tipo (valores y operaciones) no depende de su implementación. Es decir que la definición de un TAD solo depende del comportamiento descrito y que la forma en que está implementado es irrelevante para definirlo.
En el ejemplo anterior del tipo de datos de C int, la definición de la operación suma nos asegura cómo debe comportarse esta operación, sin importarnos cómo está implementada la operación o cómo está internamente representado el número entero (representación binaria en complemento a dos, representación binaria con signo, etc.).
Implementar un TAD significa elegir una representación para el conjunto de valores del tipo de datos, así como codificar sus operaciones utilizando esa representación en un lenguaje de programación. Es posible tener varias implementaciones para un mismo TAD, pero dada la definición de un TAD, el comportamiento ha de ser siempre el mismo para cualquier implementación.
La utilidad de definir TADs surge al diseñar nuevos tipos de datos. Es decir, tipos de datos que no existen como predefinidos en un lenguaje de programación. De esta forma logramos definir nuevos tipos de datos con operaciones asociadas. La idea es que el nuevo TAD solo pueda ser manipulado a través de sus operaciones. De esta forma se logra transparencia e independencia de la implementación elegida para el TAD.
1.1. Ejemplos de especificación e implementación
1.1.1. Ejemplo 19_01: números naturales
El conjunto de valores que engloba este TAD son todos los números enteros mayores o iguales a 0. Las operaciones que definiremos para aplicar a este conjunto son la suma y la división.
Implementación:
type
natural = integer;
end type
function suma(x: natural; y: natural): natural
return x+y;
end function
function division(x: natural; y:natural) : natural
return x div y;
end function
typedef unsigned int natural;
natural suma(natural x, natural y) {
return x+y;
}
natural division(natural x, natural y) {
return x/y;
}
En esta definición del tipo no se excluyen los números negativos. La responsabilidad del correcto comportamiento del tipo yace en la definición de las operaciones.
1.1.2. Ejemplo 19_02: números binarios
El conjunto de valores que engloba este TAD son todos los números en su representación binaria, es decir expresados en base 2. Las operaciones que decimos que se aplican a este conjunto de valores son: desplazamientoIzq y complemento.
Implementación:
const
MAXBITS: integer :=64;
end const
type
binari: vector[MAXBITS] of boolean;
end type
action desplazamientoIzq (inout b: binari; in n: integer)
var
i: integer;
end var
for i:=n+1 to MAXBITS do
b[i-n] := b[i];
end for
for i:=MAXBITS-n to MAXBITS do
b[i] := 0;
end for
end action
action complemento(inout b: binari)
var
i: integer;
end var
for i=1 to MAXBITS do
b[i] := not b[i];
end for
end action
#define MAXBITS 64
typedef int binario[MAXBITS];
void desplazamientoIzq(binario b, int n) {
int i;
for (i=n; i<MAXBITS; i++) {
b[i-n] = b[i];
}
for (i=MAXBITS-n; i<MAXBITS; i++) {
b[i] = 0;
}
}
void complemento(binario b) {
int i;
for (i=0; i<MAXBITS; i++) {
b[i] = !b[i];
}
}
2. TAD para representar secuencias de elementos
Una secuencia lineal es un conjunto de tamaño arbitrario de elementos del mismo tipo. Exceptuando el primero y el último, cada elemento tiene un único elemento anterior y un único posterior. Es decir que conforman una secuencia lineal.
Al hablar sobre qué podemos hacer con una secuencia, nos referimos a las operaciones que le podemos aplicar. En general un TAD que representa secuencias de elementos posee las siguientes operaciones:
- Crear la secuencia vacía.
- Insertar un elemento en la secuencia.
- Eliminar un elemento de la secuencia.
- Consultar el valor de un elemento en la secuencia.
Las respuestas a preguntas como:
¿Dónde insertar el nuevo elemento?
¿Qué elemento eliminar?
¿Qué elemento se puede consultar?
Son las que definen el comportamiento de las operaciones y, por consiguiente, el tipo de secuencia.
En esta unidad trataremos los siguientes TADs para representar secuencias: pilas, colas y listas.
2.1. El TAD Pila (stack)
2.1.1. Definición
- Una pila es una secuencia lineal de elementos
- Los elementos se insertan únicamente por un extremo de la secuencia. Por eso se dice que es una estructura LIFO (Last In First Out): el último en entrar es el primero en salir.
- La manipulación y acceso a los elementos de la pila se permite solo en un extremo de la secuencia.
Para comprender el TAD pila se puede pensar en una pila de libros dentro de una caja: el libro accesible es el que está encima de la pila. Para poder acceder a un libro en el centro de la pila, será necesario retirar todos los libros que están encima del mismo. Asimismo, el siguiente libro a apilar se colocará sobre el libro de más arriba.
Ejemplo:
Vamos a considerar el ejemplo de la pila de libros dentro de una caja. Al limpiar la caja, la pila de libros está vacía. Para ver el funcionamiento de la pila aplicaremos una serie de operaciones que se muestran en la figura 1.

Figura 1. Secuencia de operaciones sobre una pila de libros
2.1.2. Operaciones
Las operaciones que definen el TAD pila, en adelante stack se listan en la Tabla 1.
Tabla 1. Lista de operaciones sobre el TAD stack
| Operación | Descripción |
|---|---|
| createStack | Crea una pila vacía. |
| push | Empila un elemento en la pila. |
| pop | Desempila un elemento de la pila. |
| top | Devuelve una copia del elemento situado en el tope de la pila, pero sin desempilarlo. |
| emptyStack | Devuelve verdadero si la pila está vacía, falso en caso contrario. |
| fullStack | Devuelve verdadero si la pila está llena, falso en caso contrario. |
2.1.3. Implementación
La implementación propuesta se basa en un vector, donde tenemos un número máximo de elementos (MAX). Para conocer el espacio disponible de la pila en cada momento se necesita un atributo que indique el número total de elementos y que llamaremos nelem.

Figura 2. Implementación de una pila mediante un vector
Implementación del tipo:
[Ejemplo 19_03]
type
tStack = record
A: vector[MAX] of elem; {elem represents the type of the elements in the tStack}
nelem: integer;
end record
end type
typedef struct {
elem A[MAX];
int nelem;
} tStack;
Implementación de las operaciones del tipo:
Tanto en la operación de empilar (push) que se muestra en la figura 3, como en la operación de desempilar (pop) que se muestra en la figura 4, la manipulación de elementos se realiza por el extremo final de la secuencia que es también el tope de la pila.

Figura 3. Implementación de la operación push

Figura 4. Implementación de la operación pop
Implementación de las operaciones:
[Ejemplo 19_04]
function createStack() : tStack
var
s: tStack;
end var
s.nelem:= 0;
return s;
end function
action push(inout s: tStack; in e: elem)
if s.nelem = MAX then
{error full stack}
else
s.nelem:= s.nelem+1;
s.A[s.nelem]:=e;
end if
end action
action pop(inout s : tStack)
if s.nelem = 0 then
{error empty stack}
else
s.nelem:= s.nelem-1;
end if
end action
function top (s: tStack): elem
var
e: elem;
end var
if s.nelem = 0 then
{error empty stack}
else
e:= s.A[s.nelem];
end if
return e;
end function
function emptyStack (s: tStack): boolean
return s.nelem = 0;
end function
function fullStack (s: tStack): boolean
return s.nelem = MAX;
end function
#include <stdio.h>
typedef enum {FALSE, TRUE} boolean;
void createStack(tStack *s) {
s->nelem=0;
}
void push(tStack *s, elem e) {
if (s->nelem == MAX) {
printf("\n Full stack \n");
} else {
s->A[s->nelem]=e; /* first position in C is 0 */
s->nelem++;
}
}
void pop(tStack *s) {
int i;
if (s->nelem == 0) {
printf("\n Empty stack\n");
} else {
s->nelem--;
}
}
elem top(tStack s) {
elem e;
if (s.nelem == 0) {
printf("\n Empty stack \n");
} else {
e = s.A[s.nelem-1];
}
return e;
}
boolean emptyStack(tStack s) {
return (s.nelem == 0);
}
boolean fullStack(tStack s) {
return (s.nelem == MAX);
}
2.1.4. Ejemplo 19_05
Suponemos la pila de libros del ejemplo de la figura 1. Cada libro dispone de un código identificador y un nombre. Definimos las estructuras de datos necesarias para modelar el ejemplo:
type
tBook = record
name: tString;
id: integer;
end record
tBox = record
A: vector[MAX] of tBook;
nelem: integer;
end record
end type
typedef struct {
tString name;
int id;
} tBook;
typedef struct {
tBook A[MAX];
int nelem;
} tBox;
Necesitamos implementar una acción que dada una pila de libros y el código de un libro, encuentre este libro en la pila. En caso de encontrarlo, lo retiramos de la pila; en caso contrario, dejamos la pila como estaba.
[Ejemplo 19_06]
action findBook(inout s: tBox ; in id: integer)
var
b: tBook;
aux: tBox;
found: boolean;
end var
found := false;
aux := createStack();
while (not emptyStack(s) and not found) do
b := top(s);
if b.id ≠ id then
push(aux, b);
else
found := true;
end if
pop(s);
end while
while not emptyStack(aux) do
b:= top(aux);
push(s, b);
pop(aux);
end while
end action
typedef enum {FALSE, TRUE} boolean;
void findBook(tBox *s, int id) {
tBook b;
tBox aux;
boolean found;
int i;
found = FALSE;
createStack(&aux);
while (!emptyStack(*s) && !found) {
b = top(*s);
if (b.id != id) {
push(&aux, b);
} else {
found = TRUE;
}
pop(s);
}
while (!emptyStack(aux)) {
b = top(aux);
push(s, b);
pop(&aux);
}
}
2.2. El TAD Cola (queue)
2.2.1. Definición
- Una cola es una secuencia lineal de elementos
- Los elementos se insertan por el final de la cola y se extraen por el principio de la cola. Por eso se dice que es una estructura FIFO (First In First Out): el primero en entrar es el primero en salir, ya que los elementos se extraen de la cola en el mismo orden en el que se han insertado.
- La manipulación y el acceso a los elementos de la cola solo se permite en los extremos.
Para comprender el TAD cola se puede pensar en una cola de personas esperando para comprar una entrada en la taquilla de un teatro: la primera persona que está en la cola es la primera en ser atendida, las personas que llegan se unen al final de la cola.
Ejemplo 19_07
Vamos a considerar la cola de una taquilla. Cuando abre la taquilla creamos la cola vacía y, para ver su funcionamiento, aplicaremos una serie de operaciones tal como se muestra en la figura 5.

Figura 5. Secuencia de operaciones sobre una cola de personas en una taquilla de teatro
2.2.2. Operaciones
Las operaciones que definen el TAD pila, en adelante queue se listan en la tabla 2.
Tabla 2. Lista de operaciones sobre el TAD queue
| Operación | Descripción |
|---|---|
| createQueue | Crea una cola vacía. |
| enqueue | Inserta un elemento en la cola. |
| dequeue | Elimina un elemento de la cola. |
| head | Devuelve el elemento situado al comienzo de la cola. |
| emptyQueue | Devuelve verdadero si la cola está vacía, falso en caso contrario. |
| fullQueue | Devuelve verdadero si la cola está llena, falso en caso contrario. |
2.2.3. Implementación
La implementación propuesta se basa en un vector, donde tenemos un número máximo de elementos (MAX). Para conocer el espacio disponible en la cola en cada momento se necesita un atributo que indique el número total de elementos y que llamaremos nelem.
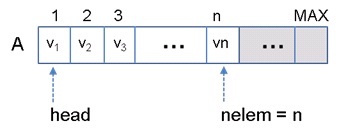
Figura 6. Implementación de una cola mediante un vector
Tal como se muestra en la figura 6, el primer elemento de la cola se almacena en la posición 1 del vector y el último en la posición nelem que representa el final de la cola.
Implementación del tipo:
type
queue = record
A: vector[MAX] of elem;
nelem: integer;
end record
end type
typedef struct {
elem A[MAX];
int nelem;
} queue;
Implementación de las operaciones:
Los elementos se encolan (operación enqueue) por el final de la cola y se desencolan (operación dequeue) por el principio de la cola (posición 1). Tened en cuenta que cada vez que se elimina un elemento se han de desplazar todos los elementos de la cola una posición hacia la izquierda según se muestra en la figura 7.

Figura 7. Implemetación de la operación dequeue
Implementación de las operaciones:
[Ejemplo 19_08]
function createQueue() : queue
var
q : queue;
end var
q.nelem := 0;
return q;
end function
action enqueue(inout q: queue; in e: elem)
if q.nelem = MAX then
{error full_queue}
else
q.nelem := q.nelem+1;
q.A[q.nelem]:=e;
end if
end action
action dequeue(inout q : queue)
var
i: enter;
end var
if q.nelem = 0 then
{error empty_queue}
else
for i:=1 to q.nelem-1 do
q.A[i] := q.A[i+1];
end for
q.nelem := q.nelem - 1;
end if
end action
function head (q: queue): elem
var
e: elem
end var
if q.nelem = 0 then
{error empty_queue}
else
e:= q.A[1];
end if
return e;
end function
function emptyQueue(q:queue): boolean
return (q.nelem = 0);
end function
function fullQueue(q:queue): boolean
return (q.nelem = MAX);
end function
#include <stdio.h>
typedef enum {FALSE, TRUE} boolean;
void createQueue(queue *q) {
q->nelem=0;
}
void enqueue(queue *q, elem e) {
if (q->nelem == MAX) {
printf("\n Full queue \n");
} else {
q->A[q->nelem]=e; /* first position in C is 0 */
q->nelem++;
}
}
void dequeue(queue *q) {
int i;
if (q->nelem == 0) {
printf("\n Empty queue\n");
} else {
for (i=0; i < q->nelem-1; i++) {
q->A[i] = q->A[i+1];
}
q->nelem--;
}
}
elem head(queue q) {
elem e;
if (q.nelem == 0) {
printf("\n Empty queue \n");
} else {
e = q.A[0];
}
return e;
}
boolean emptyQueue(queue q) {
return (q.nelem == 0);
}
boolean fullQueue(queue q) {
return (q.nelem == MAX);
}
2.2.4. Ejemplo 19_09
Supongamos la cola de la taquilla del ejemplo de la figura 5. Cada cliente de la cola tiene asociado el ordinal en la cola desde que abrió la taquilla y la cantidad de entradas que desea adquirir. Definimos las estructuras de datos necesarias para modelar el ejemplo:
type
tClient = record
num: integer;
quantity: integer;
end record
tTicketWin = record
A: vector[MAX] of tClient;
nelem: integer;
end record
end type
typedef struct {
int num;
int quantity;
} tClient;
typedef struct {
tClient A[MAX];
int nelem;
} tTicketWin;
Necesitamos implementar una acción que atienda el primer cliente de la cola en la taquilla. La acción recibe como parámetros la cola q de clientes y un número available que indica la disponibilidad de entradas. En caso de haber suficientes entradas disponibles, se actualiza la cantidad de entradas disponibles y se devuelve el valor verdadero en el parámetro sold. Una vez el cliente es atendido, se elimina de la cola.
[Ejemplo 19_10]
action serveClient (inout q: tTicketWin, inout available: integer, out sold : boolean)
var
c: tClient;
end var
sold := false;
if not emptyQueue(q) then
c:= head(q);
if c.quantity ≤ available then
available := available - c.quantity;
sold := true;
end if
dequeue(q);
end if
end action
typedef enum {FALSE, TRUE} boolean;
void serveClient(queue *q, int *available, int *sold) {
elem c;
*sold = FALSE;
if (!emptyQueue(*q)) {
c= head(*q);
if (c.quantity <= *available) {
*available = *available - c.quantity;
*sold = TRUE;
}
dequeue(q);
}
}
2.3. El TAD Lista (list)
2.3.1. Definición
- Una lista es una secuencia lineal de elementos.
- Es posible insertar, eliminar y consultar elementos en cualquier posición de la secuencia.
Para comprender el TAD lista se puede pensar en la lista de compra del supermercado, en una lista de direcciones, en una lista de deseos para el año nuevo,...
Ejemplo 19_11
Vamos a considerar la lista de la compra: leche, azúcar, arroz; donde leche es el primer elemento. Para construir la lista, primero creamos una lista vacía y luego aplicamos una serie de operaciones hasta obtener la lista completa tal como se muestra en la figura 8.

Figura 8. Secuencia de operaciones para construir una lista de la compra del supermercado
2.3.2. Operaciones
Las operaciones que definen el TAD lista, en adelante list se listan en la Tabla 3.
Tabla 3. Lista de operaciones sobre el TAD list.
| Operación | Descripción |
|---|---|
| createList | Crea una cola vacía. |
| insert | Inserta un elemento en la lista. |
| delete | Elimina un elemento de la lista. |
| get | Devuelve el elemento situado en una posición dada de la lista. |
| end | Devuelve verdadero si la posición dada es posterior a la última, falso en caso contrario. |
| emptyList | Devuelve verdadero si la lista está vacía, falso en caso contrario. |
| fullList | Devuelve verdadero si la lista está llena, falso en caso contrario. |
2.3.3. Implementación
La implementación propuesta se basa en un vector, donde tenemos un número máximo de elementos (MAX). Para conocer en cada momento el espacio disponible en la lista se necesita un atributo que indique el número total de elementos y que llamaremos nelem.

Figura 9. Implementación de una lista mediante un vector
Implementación del tipo:
type
list = record
A: vector[MAX] of elem;
nelem: integer;
end record
end type
typedef struct {
elem A[MAX];
int nelem;
} list;
Implementación de las operaciones:'''
Tanto la inserción de elementos (operación insert) como el borrado (operación delete) se pueden realizar en cualquier posición de la lista.
Cada vez que se inserta un nuevo elemento, salvo que sea al final de la lista, habrá que hacer espacio para ubicar el nuevo elemento. Por este motivo será necesario desplazar todos los elementos un lugar hacia la posición siguiente. En la figura 10 se muestra cómo se realiza una inserción de un elemento en la posición 5 del vector.

Cuando se elimina un elemento, el espacio generado por el elemento borrado se llena desplazando todos los elementos hacia una posición más baja. En la figura 11 se muestra el borrado de un elemento en la posición 3 de un vector.

Implementación de las operaciones:
[Ejemplo 19_12]
function createList() : list
var
l : list;
end var
l.nelem := 0;
return l;
end function
action insert(inout l: list; in e:elem; in index: integer)
var
i: integer;
end var
if l.nelem = MAX then
{error full list}
else
for i:=l.nelem-1 to index step -1do
l.A[i+1]:= l.A[i];
end for
l.nelem := l.nelem+1;
l.A[index]:=e;
end if
end action
action delete(inout l: list; in index: integer)
var
i: integer;
end var
if l.nelem = 0 then
{error empty list}
else
for i:=index to q.nelem-1 do
l.A[i] := l.A[i+1];
end for
l.nelem := l.nelem-1;
end if
end action
function get(l: queue; index: integer): elem
var
e: elem
end var
if l.nelem = 0 then
{error empty list}
else
e:= l.A[index];
end if
return e;
end function
function end(l: list; pos: integer): boolean
return (pos > l.nelem);
end function
function emptyList(l:list): boolean
return (l.nelem = 0);
end function
function fullList(l:list): boolean
return (l.nelem = MAX);
end function
#include <stdio.h>
typedef enum {FALSE, TRUE} boolean;
void createList(list *l) {
l->nelem = 0;
}
void insert(list *l, elem e, int index) {
int i;
if (l->nelem == MAX) {
printf("\n Full list \n");
} else {
for (i=l->nelem-1; i>=index; i--) {
l->A[i+1] = l->A[i];
}
l->nelem++;
l->A[index]=e;
}
}
void delete(list *l, int index) {
int i;
if (l->nelem == 0) {
printf("\n Empty list\n");
} else {
for (i=index; i<l->nelem-1; i++) {
l->A[i] = l->A[i+1];
}
l->nelem--;
}
}
elem get(list l, int index) {
elem e;
if (l.nelem == 0) {
printf("\n Empty list \n");
} else {
e=l.A[index];
}
return e;
}
boolean end(list l, int pos) {
return (pos >= l.nelem);
}
boolean emptyList(list l) {
return (l.nelem == 0);
}
boolean fullList(list l) {
return (l.nelem == MAX);
}
2.3.4. Ejemplo 19_13
Suponemos la lista de la compra de la figura 8. Cada artículo de la lista tiene asociado un nombre, el tipo de artículo clasificado según sea de panadería, frescos, bebidas, congelados, belleza o desayuno y la cantidad de este artículo que comprar. Definimos las estructuras de datos necesarias para modelar el ejemplo:
type
tArticleType = {bakery, fresh, drinks, frozen, beauty, breakfast}
tArticle = record
type: tArticleType;
quantity: real;
end record
tBuyList = record
A: vector[MAX] of tArticle;
nelem: integer;
end record
end type
typedef enum {bakery, fresh, drinks, frozen, beauty, breakfast} articleType;
typedef struct {
articleType type;
float quantity;
} tArticle;
typedef struct {
tArticle A[MAX];
int nelem;
} tBuyList;
Necesitamos implementar una acción que elimine de la lista de la compra l, todos los artículos de un tipo dado (filter) que se recibe como parámetro.
[Ejemplo 19_14]
action filterArticleType (inout l : tBuyList; in filter: tArticleType)
var
a: tArticle;
pos: integer;
end var
pos:=1;
while pos ≤ l.nelem do
a:= get(l, pos);
if a.type = filter then
delete(l, pos);
end if
pos := pos+1;
end while
end action
void filterArticleType(list *l , articleType filter) {
elem a;
int pos;
pos=0;
while (pos < l->nelem) {
a= get(*l, pos);
if (a.type == filter) {
delete(l, pos);
}
pos = pos+1;
}
}
Resumen
En esta unidad hemos visto qué significa un tipo abstracto de datos (TAD) y su utilidad en la programación.
Hemos visto algunos ejemplos de TADs simples y complejos. En este último punto hemos visto cómo definir tres tipos de TADs diferentes para representar secuencias: pila, cola y lista.
Se ha visto también la implementación del tipo secuencia utilizando vectores, así como la implementación de sus operaciones utilizando esta implementación del tipo. Para cada uno de los tipos de secuencia hemos visto un ejemplo de aplicación implementado.