14. Modularidad
Objetivos
- Entender la utilidad de las acciones y funciones.
- Comprender la diferencia entre acción y función.
- Entender que es un parámetro actual y distinguirlo del parámetro formal.
- Saber definir acciones y funciones y saberlas llamar.
- Distinguir entre las implicaciones de pasar parámetros de entrada a pasarlos de salida.
- Comprender el concepto de modularización de los algoritmos.
Introducción
Los algoritmos que hemos visto hasta el momento han sido algoritmos sencillos donde se han utilizado asignaciones y estructuras de control tanto alternativas (para tomar decisiones) como iterativas (para repetir acciones hasta que se cumpla una condición).
Estas estructuras nos permiten escribir algoritmos simples, pero cuando los algoritmos se complican, la escritura de un algoritmo secuencial y su posterior comprensión y mantenimiento se pueden complicar mucho.
1. Aproximación intuitiva
Pensemos, por ejemplo, en una comida que queramos hacer en casa. Tenemos dos opciones, hacer una a una todas las tareas necesarias para cocinar todo lo que necesitamos o bien podemos encargar a diferentes especialistas los distintos platos que necesitamos.
Si queremos hacer un algoritmo de preparación del menú, en el caso de hacerlo todo nosotros deberíamos especificar todos los pasos para cocinar todos los platos. Tendríamos un algoritmo largo que describiría la elaboración de cada plato. En cambio, si tomamos la segunda opción, el algoritmo quedaría bastante más sencillo.
Supongamos, por ejemplo, que el menú que queremos consiste en paella, bacalao con ajoaceite y pastel. Si optamos por la segunda vía, el algoritmo podría quedar más a o menos como sigue:
[Ejemplo 14_01]
algorithm almuerzo
var
primerPlato, salsa, segundoPlato, postres: tPlato;
end var
primerPlato:= encargarPaella(marisco, 5);
segundoPlato:= encargarPescado(bacalao, all_i_oli, 5);
postres:= encargarPostres(pastel, chocolate, velas, 5);
end algorithm
Comentarios:
- Hemos supuesto que tPlato es un tipo de variable de nuestro entorno de definición de algoritmos de cocina.
- Para pedir cada uno de los platos, hemos puesto entre paréntesis las indicaciones de cómo queremos el plato. Marisco y para 5 para la paella para indicar que la queremos de marisco y para 5 personas. Bacalao, ajoaceite y 5 para indicar el tipo de pescado, la salsa y el número de personas y lo mismo para los postres.
- El especialista ha determinado las opciones que nosotros debemos elegir y nosotros debemos dar valor a estas opciones al hacer el encargo. Los cocineros de paella solo nos dejan elegir el tipo de paella y los comensales. Los suministradores de platos de pescado, en cambio, además de las personas y el tipo de pescado también nos permiten elegir una salsa. El pastelero deja más opciones a decidir a quién hace el encargo.
Para que podamos usar a un especialista debemos saber qué datos comunicarle para hacer un encargo correcto.
Podemos ver cómo nuestro algoritmo, a base de solicitar a expertos que hagan el trabajo, se convierte en un algoritmo simple y fácil de entender. Lo único que hemos tenido que hacer son peticiones en las que hemos añadido valores, a los que llamamos parámetros, que indican exactamente cómo queremos cada plato.
Además, con este sistema, la receta (algoritmo) exacto que hay detrás de cada plato, mientras cumpla con lo esperado, nos da igual cuál sea. Si algún cocinero decide cambiar la receta, para mejorarla, nos da igual siempre y cuando el resultado se mantenga.
Los lenguajes de programación permiten trabajar de una forma similar a como lo hemos hecho en nuestro menú. Es decir, se pueden utilizar subalgortimos, o se pueden definir otros nuevos, que quedan aparte del algoritmo principal y que permiten dividir un algoritmo complicado en subalgoritmos más simples. Además, como veremos en los siguientes apartados, otra de las ventajas que proporcionan es el hecho de que estos subalgoritmos se pueden reutilizar evitando la reescritura de código.
Estos subalgoritmos reciben el nombre de acciones y funciones y es como si empaquetásemos un conjunto de instrucciones que resuelven un problema y no nos tenemos que preocupar de lo que hay dentro.
De hecho, en las unidades anteriores ya se han utilizado. Por ejemplo,
- Al leer o escribir datos. La lectura y escritura de datos debe usar llamadas al sistema operativo, que es como interactúa el programa con el ordenador en concreto que estamos usando. Para poder escribir algoritmos que no dependan del SO, los lenguajes de programación ofrecen acciones o funciones para realizar esta tarea. Nos independizan del mismo. Por ejemplo, hemos usado:
- En lenguaje algorítmico hemos usado i=readInteger(), y en C scanf("%d", &i) para leer un número entero.
Podéis ver el apartado de acciones y funciones predefinidas para ver una lista de algunas de las acciones y funciones más comunes que ya vienen definidas con los lenguajes de programación.
- O, por ejemplo, cuando se ha utilizado switchOnAirConditioning() en la unidad de la estructura alternativa, donde se da por supuesto que hay un subalgoritmo que realiza la acción de encender el aire acondicionado.
Veamos con un ejemplo cómo podemos mejorar un algoritmo usando este concepto.
1.1. Ejemplo - Cálculo de combinaciones
Supongamos que tenemos que diseñar un algoritmo que permita saber cuántas combinaciones de colores se pueden hacer si disponemos de n telas, cada una de un color diferente. Concretamente se quiere disponer de un algoritmo genérico que dados n colores calcule cuantas combinaciones se pueden hacer utilizando cada vez m colores, donde m y n son enteros y m ≤ n.
Recordemos que la fórmula matemática para calcular las combinaciones viene dada por el número combinatorio y que se calcula de la siguiente manera:
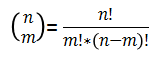
Diseñemos primero la solución sin preocuparnos del cálculo del factorial, que ya hemos visto en la unidad de estructuras iterativas.
Para diseñar el algoritmo deberemos leer los valores de n y m y haberlo indicado en la fórmula. Quedaría:
[Ejemplo 14_02]
algorithm combinations
var
{definimos las variables, dos enteros que hay que leer y una donde almacenar el resultado}
totalNumColors, colorsToCombine: integer ;
result: integer;
end var
{leemos los dos números}
totalNumColors:= readInteger();
colorsToCombine:= readInteger();
{Hacemos un esbozo del cálculo, suponiendo que disponemos de una manera de calcular el factorial de un número }
result := totalNumColors! div (colorsToCombine! * (totalNumColors-colorsToCombine)!) ;
writeInteger(result);
end algorithm
int main() {
int totalNumColors;
int colorsToCombine;
int result;
result = totalNumColors! div (colorsToCombine! * (totalNumColors-colorsToCombine)!) ;
printf ("%d ", result);
return 0;
}
Como podemos ver, si suponemos que tenemos una manera de calcular el factorial, nos queda un diseño simple y fácil de entender.
Ahora bien, como hemos visto previamente, el cálculo del factorial no es tan simple como una sola línea de código. Para calcularlo se necesita hacer una iteración para ir calculando el producto de todos los enteros, además de la necesidad de variables donde guardar los cálculos parciales. Recordemos cómo se calculaba:
[Ejemplo 14_03]
var
factorial: integer;
i: integer;
n: integer;
end var
n:= readInteger();
factorial:= 1;
i:=1;
while i ≤ n do
factorial:=factorial*i;
i:=i+1;
end while
int main() {
int factorial;
int i;
int n;
scanf("%d", &n);
factorial=1;
i=1;
while(i <= n) {
factorial = factorial*i;
i++;
}
return 0;
}
Si incorporamos el cálculo del factorial a nuestro algoritmo vemos que para calcularlo necesitamos varias líneas de código que, además, se deben repetir tres veces para calcular cada uno de los factoriales. El algoritmo quedaría:
[Ejemplo 14_04]
algorithm combinations
var
{definimos las variables, dos enteros que hay que leer , una donde almacenar el resultado y variables para los tres factoriales}
totalNumColors, colorsToCombine: integer ;
factorial1: integer;
factorial2: integer;
factorial3: integer;
i: integer;
result: integer;
end var
{leemos los números}
totalNumColors:= readInteger();
colorsToCombine:= readInteger();
{calculamos los factoriales}
factorial1:=1;
i:=1;
while (i ≤ totalColorsToCombine) do
factorial1:= factorial1*i;
i:= i+1;
end while
factorial2:=1;
i:=1;
while (i ≤ colorsToCombine) do
factorial2:= factorial2*i;
i:= i+1;
end while
factorial3:=1;
i:=1;
while (i≤ (totalColorsToCaombine - colorsToCombine)) do
factorial3:=factorial3*i;
i:=i+1;
end while
{Calculamos el resultado final}
result := factorial1 div (factorial2 * factorial3) ;
writeInteger(result);
end algorithm
int main() {
int totalNumColors, colorsToCombine;
int factorial1;
int factorial2;
int factorial3;
int i;
int result;
totalNumColors = readInteger();
colorsToCombine = readInteger();
factorial1 = 1;
i = 1;
while ( i <= totalColorsToCombine) {
factorial1 = factorial1*i;
i++;
}
factorial2 = 1;
i = 1;
while ( i <= colorsToCombine) {
factorial2 = factorial2*i;
i++;
}
factorial3 = 1;
i = 1;
while ( i <= totalColorsToCaombine - colorsToCombine) {
factorial3 = factorial3*i;
i++;
}
result = (int) factorial1 / (factorial2 * factorial3) ;
printf("%d ", result);
return 0;
}
Por lo tanto, escribir el algoritmo completo solamente con los elementos básicos del lenguaje algorítmico implica que un diseño aparentemente simple se complique teniendo que sustituir, como pasa en nuestro ejemplo, una división por muchas líneas de código que son, además, repetitivas.
En cambio, si diseñamos un subalgoritmo que calcule el factorial y que podamos usar pasándole un parámetro, como hemos hecho en el ejemplo de la paella, podemos seguir utilizando el diseño original, que es más fácil de entender.
En esta unidad estudiamos estos elementos del lenguaje algorítmico:
- Cómo definir estos subalgoritmos que llamamos funciones y acciones.
- Cómo utilizarlos desde el algoritmo principal o desde otras acciones y funciones.
- Cómo puede comunicarse el algoritmo principal con las acciones o funciones con las que se comunica. En otras palabras, cómo puede pasar y recibir información (lo que llamamos parámetros).
- En qué se diferencian las acciones de las funciones.
- Cómo el uso de acciones y funciones, aparte de evitar la reescritura de código, permite resolver los problemas de una manera modular y estructurada.
2. Funciones
Una función es un conjunto independiente de instrucciones que resuelven una tarea concreta, que devuelve un valor y que puede ser referenciada (invocada o llamada) desde otro punto de un algoritmo.
De hecho, podemos ver una función como si fuese un subalgoritmo, con la ventaja de que se puede llamar (utilizar) tantas veces como se quiera.
2.1. Sintaxis para la declaración de una función
Antes de ver la sintaxis para la declaración de una función, pensemos en qué elementos serán necesarios para definirla:
- Un nombre para poder identificarla.
- Una serie de valores sobre los que se quieren hacer los cálculos. Por ejemplo, en el caso que hemos visto del factorial, deberíamos indicar el número sobre el que se quiere hacer el cálculo. Estos valores reciben el nombre de parámetros formales de la función. Para cada parámetro es necesario indicar su nombre y su tipo, como si se declarasen variables. De hecho, los parámetros actúan como variables dentro de la función.
- Las instrucciones propiamente dichas que hay que hacer en la función, es decir, el cuerpo de la función.
- El valor resultante de la función, en nuestro ejemplo, el resultado de calcular el factorial. Hay que indicar el tipo de resultado que devuelve la función.
Así pues, la sintaxis para declarar una función es la siguiente:
[Ejemplo 14_05]
function name(param1: type1 , param2: type2, ..., paramn: typen): returnType
...
...
return expression;
end function
...
...
/* returnValue es el valor que calcula la función */
return returnValue
}
En esta declaración es importante lo que llamamos la cabecera de la función. La cabecera es la parte que describe cómo debe llamarse a una función. Indica su nombre, los parámetros que espera para ejecutarse correctamente y el tipo que retorna.
Concretamente, la cabecera tiene la siguiente estructura:
[Ejemplo 14_06]
function name(param1: type1 , param2: type2, ..., paramn: typen): returntype
returnType name(type1 param1, type2 param2, ..., typen param);
Podemos ver que, a excepción del cuerpo de la función, la cabecera contiene todos los elementos que hemos identificado como necesarios para definirla.
Siguiendo con nuestro ejemplo del factorial, la función sería:
[Ejemplo 14_07]
function factorial (number: integer): integer
var
fact: integer;
i: integer;
end var
fact:= 1;
i:=1;
while i ≤ number do
fact:= fact*i;
i:= i+1;
end while
return(fact);
end function
int factorial(int number) {
int fact;
int i;
fact=1;
i=1;
while(i <= number) {
fact = fact*i;
i++;
}
return fact;
}
Donde hemos utilizado:
- el nombre factorial para identificar la función;
- un único parámetro, en este caso un entero, para identificar el número sobre el que queremos hacer el cálculo del factorial;
- el tipo de retorno, que también será entero
- y el cuerpo de la función, que hace los cálculos.
Un par de comentarios sobre las variables y los parámetros:
- Dentro de la función, solamente se pueden utilizar las variables definidas dentro de la misma y los parámetros formales, que actúan como variables.
- En una función, si se modifica el valor de un parámetro formal, dicha modificación no tiene ningún impacto fuera de la función.
2.2. Cómo utilizar (llamar) a una función
Una vez definida la función esta se puede utilizar desde el algoritmo principal o desde otra función.
Cuando se llama a una función, el control de la ejecución de las instrucciones pasa a la función. Esta ejecuta el código definido hasta alcanzar el fin de la función. Entonces el control vuelve al punto donde la función ha sido llamada.
Para llamar a una función se debe poner su nombre, seguido de un paréntesis, la lista de valores que se quieren pasar como parámetros y un paréntesis para cerrar. Los parámetros utilizados en la llamada reciben el nombre de parámetros actuales (o reales). El número de parámetros actuales debe coincidir en número y orden con los parámetros y tipos definidos en la cabecera.
Los parámetros actuales de una función pueden ser constantes, variables o expresiones.
A continuación, vemos cómo se llama a una función a partir de su cabecera.
[Ejemplo 14_08]
{Si suponemos que tenemos la siguiente cabecera}
function name(param1: integer , param2: real, param3: char): integer;
{y suponemos que tenemos la declaración de las siguientes variables}
var
a: integer;
b: real;
c: char;
result: integer;
end var
{La manera de llamar a la función sería:}
result:= name(a, b, c);
int name(int param1, float param2, char param3);
//Y suponemos que tenemos la declaración de las siguientes variables:
int a;
float b;
char c;
int reault;
//La manera de llamar a la función en C sería:
result= name(a, b, c);
Los objetos utilizados en la llamada se llaman parámetros actuales o reales. Es decir, en el ejemplo, las variables a, b y c son los parámetros actuales. En las funciones, los parámetros actuales pueden ser variables, constantes o expresiones.
En el caso del factorial, recordemos que la cabecera era:
function factorial (number: integer): integer;
Es decir, tiene un único parámetro formal de tipo entero. Por lo tanto, suponiendo que n, m y p son tres variables de tipo entero, las posibles maneras de llamar a la función serían:
n:= factorial(5); /* utilizando una constante como parámetro actual*/
n:= factorial(p) /* utilizando una variable como parámetro actual */
n:= factorial(m+2) /* utilizando una expresión como parámetro actual */
El algoritmo completo en el caso del factorial sería:
[Ejemplo 14_09]
function factorial (number: integer): integer
var
fact: integer;
i: integer;
end var
fact:= 1;
i:=1;
i:=1;
while i ≤ number do
fact:=fact*i;
i:=i+1;
end while*
return(fact);
end function
algorithm combinations
var
{definimos las variables, dos enteros que hay que leer y una donde almacenar el resultado }
totalNumColors, colorsToCombine: integer ;
result: integer;
end var
{leemos los números}
totalNumColors:= readInteger();
colorsToCombine:= readInteger();
result := factorial(totalNumColors) div ( factorial(colorsToCombine) * factorial(totalNumColors-colorsToCombine));
writeInteger(result);
end algorithm
#include <stdio.h>
int factorial(int number) {
int fact;
int i;
fact= 1;
i=1;
while(i <= number) {
fact = fact*i;
i++;
}
return fact;
}
int main() {
int totalNumColors;
int colorsToCombine;
int result;
scanf("%d", &totalNumColors);
scanf("%d", &colorsToCombine);
result = factorial(totalNumColors) / ( factorial(colorsToCombine) * factorial(totalNumColors-colorsToCombine));
printf ("%d ", result);
return 0;
}
Donde hemos sustituido la expresión matemática m, que no forma parte del lenguaje algorítmico, por la llamada correcta a la función que es factorial(m).
3. Acciones
Hemos visto que una función es un subalgoritmo que recibe unos parámetros y retorna un valor. De hecho, una función tiene una mecánica de funcionamiento similar a la de una función matemática.
Pero, a veces, interesa tan solo disponer de un subalgoritmo que realice una serie de instrucciones, pero que no necesariamente devuelva un valor en el sentido matemático. Para estas situaciones, el lenguaje algorítmico generaliza el concepto de función y define el concepto de acción.
Una acción es un conjunto independiente de instrucciones que resuelven una tarea concreta y que puede ser referenciada (invocada o llamada) desde otro punto del algoritmo.
Una acción se diferencia de una función porque:
- No retorna ningún valor.
- Cuando modifica un parámetro formal, puede estar también modificando el parámetro actual, como veremos en el siguiente apartado.
3.1. Sintaxis para la declaración de una acción
Al igual que una función, una acción necesita:
- Un nombre para identificarla.
- Una serie de valores sobre los que se quieren hacer los cálculos. Estos valores se llaman parámetros formales de la acción. Para cada parámetro habrá que indicar su nombre y su tipo y, además, el modo en el que se comunica este parámetro. Los parámetros actúan como variables dentro de la acción.
- Las instrucciones que deben ejecutarse dentro de la acción, es decir, el cuerpo de la acción.
La sintaxis para definir una acción es igual a la de la función excepto por dos cosas:
- La acción no tiene tipo de retorno, ya que no retorna ningún valor.
- En una acción hay que indicar delante del nombre del parámetro cómo se pasa. Utilizamos las palabras in, out e inout para indicar si el parámetro es de entrada, salida o entrada/salida, es decir, cómo se comunica. En la siguiente sección se explican los distintos modos de pasar los parámetros a una acción.
[Ejemplo 14_10]
action name(class1 param1: type1 , class2 param2: type2, ..., classn paramn: typen)
...
...
end action
...
...
}
4. Tipos de parámetros
En las funciones ya hemos visto cómo se pasa uno de los tipos de parámetros tal como se hace en las funciones matemáticas. Es decir, unos valores que la función utiliza para hacer los cálculos. Ahora bien, como vamos a ver a continuación, hay otras maneras de pasar los parámetros y, según el método que se use, el comportamiento será diferente.
- Parámetro de entrada. El valor del parámetro solamente será consultado y utilizado dentro de la acción. Esta manera de pasar parámetros es típica de funciones matemáticas y es la única manera que puede usarse en las funciones. En los ejemplos que hemos visto hasta ahora, todos los parámetros definidos han sido de entrada. Como en la acción solo se usará como un valor, una constante, una variable o una expresión puede ser parámetro de entrada.
- Parámetro de salida. Se utiliza para asignar un valor al parámetro. Si el parámetro ya tiene un valor inicial, este valor no se debería utilizar dentro de la acción. Normalmente se pasan los parámetros de esta manera para que sean inicializados por la acción. Puesto que la acción dejará un valor en el parámetro, este debe ser obligatoriamente una variable.
- Parámetros de entrada/salida. Se utilizan para actualizar el valor del parámetro. En este caso, el valor inicial del parámetro se puede utilizar y también se puede modificar, devolviendo un nuevo valor a quien ha llamado a la acción. Puesto que la acción dejará un nuevo valor en el parámetro, este debe ser obligatoriamente una variable.
Los siguientes ejemplos muestran cómo se modifican tanto los parámetros actuales como formales según el modo en que se pasen los parámetros.
4.1. Ejemplo 14_11: parámetros de entrada
Supongamos que disponemos de una acción que, dados el número de piezas compradas a un mayorista y el precio por pieza, calcula el coste total y lo muestra por el canal estándar, teniendo en cuenta que según el número de piezas, se aplicará un tipo de descuento u otro.
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
end const
algorithm example1
var
num: integer;
price: real;
end var
num:= 1005;
price:= 10.0;
computeCost(num, price);
end algorithm
action computeCost(in num: integer, in price: real)
var
val: real;
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= integerToReal(num) * price * (1.0 - discount);
writeReal(val);
end action
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
void computeCost(int num, float price) {
float val;
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
val = (float) (num)*price* (1.0 - discount);
printf("%f", val);
}
int main() {
float price;
int num;
num = 1005;
price = 10.0;
computeCost(num, price);
return 0;
}
El estado de las variables y parámetros antes y después de ejecutar la función se presenta en el siguiente dibujo:
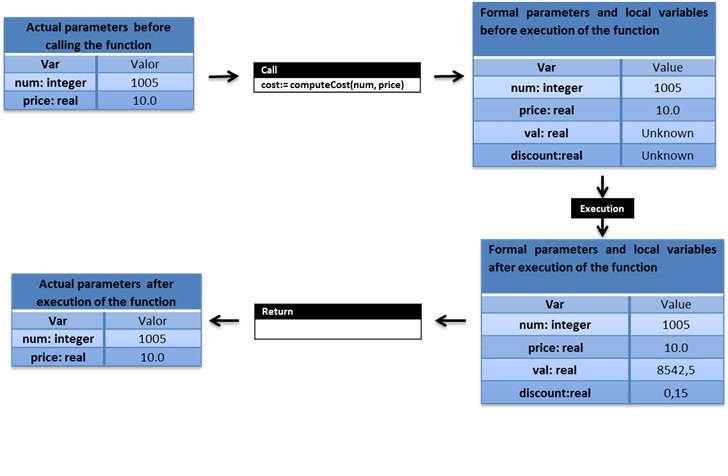
Comentarios:
- Aunque los parámetros formales y actuales tengan el mismo nombre, se trata de variables diferentes.
- Podemos ver que los parámetros actuales no han cambiado.
4.2. Ejemplo 14_12: parámetros de salida
Supongamos ahora el mismo ejemplo, pero con una acción que tiene un parámetro de salida para devolver el coste:
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
end const
algorithm example2
var
num: integer;
price: real;
cost: real;
end var
num:= 1005;
price:= 10.0;
computeCost(num, price, cost);
writeReal(cost);
end algorithm
action computeCost(in num: integer, in price: real, out val: real);
var
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= integerToReal(num) * price * (1.0 - discount);
end action
#include <stdio.h>
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
void computeCost(int num, float price, float *val) {
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
*val = (float) (num)*price* (1.0 - discount);
}
int main() {
float price;
int num;
float cost;
num = 1005;
price = 10.0;
computeCost(num, price, &cost);
printf("%f", cost);
return 0;
}
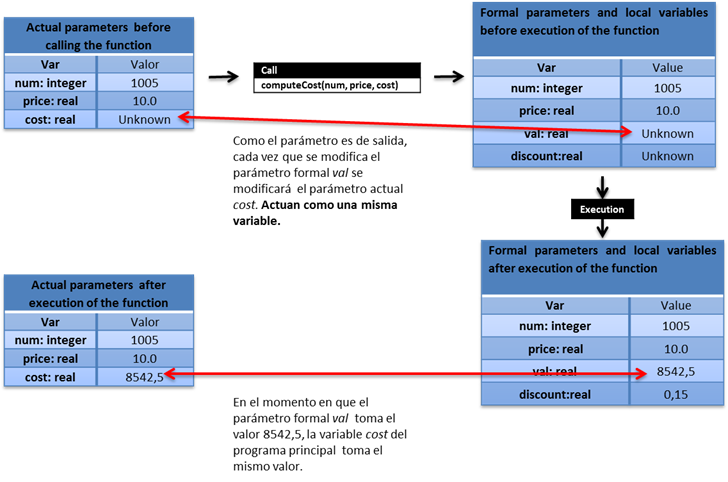
Comentarios:
- Al tratarse de una acción, se llama sin asignar el retorno a una variable, ya que las acciones no retornan ningún valor.
- La acción tiene un parámetro formal de salida. Esto quiere decir que cada vez que se modifique este parámetro dentro de la acción, automáticamente se modificará con el mismo valor el parámetro actual correspondiente cost.
- Podemos ver que en lenguaje C, los parámetros de salida son en realidad punteros. Más adelante se muestra un ejemplo.
4.3. Ejemplo 14_13: parámetros de entrada y salida
Supongamos ahora que el coste final es la suma de unos gastos mínimos (coste de entrega, etc.) más el coste de venta. El coste mínimo viene dado por una constante BASIC_COST.
const
MAX_DISCOUNT: real = 0.15;
MIN_DISCOUNT: real = 0.05;
LIMIT: integer = 1000;
BASIC_COST: real = 100.0;
end const
algorithm example3
var
num: integer;
price: real;
cost: real;
end var
num:= 1005;
price:= 10.0;
cost:= BASIC_COST;
computeCost(num, price, cost);
writeReal(cost);
end algorithm
action computeCost(in num: integer, in price: real, inout val: real);
var
discount: real;
end var
if num ≥ LIMIT then
discount:= MAX_DISCOUNT;
else
discount:= MIN_DISCOUNT;
end if
val:= val + integerToReal(num) * price * (1.0 - discount);
end action
#define MAX_DISCOUNT 0.15
#define MIN_DISCOUNT 0.05
#define LIMIT 1000
#define BASIC_COST 100.0
void computeCost(int num, float price, float *val) {
float discount;
if (num >= LIMIT) {
discount = MAX_DISCOUNT;
} else {
discount = MIN_DISCOUNT;
}
*val = *val + (float) (num) * price * (1.0 - discount);
}
int main() {
float price;
int num;
float cost;
num = 1005;
price = 10.0;
cost = BASIC_COST;
computeCost(num, price, &cost);
printf("%f", cost);
return 0;
}
La imagen siguiente muestra el estado de los parámetros y las variables:
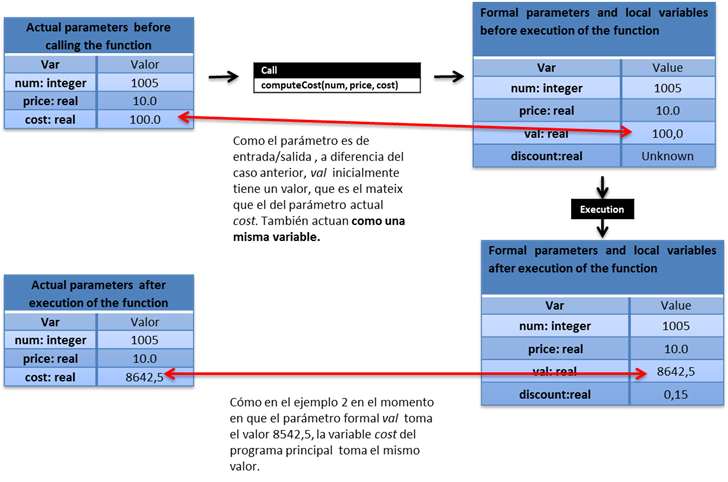
Comentarios:
- La única diferencia con el ejemplo 2 es que el parámetro val ahora es de entrada y salida y su valor se actualiza sumándole el coste de venta.
- Por lo demás, los parámetros de entrada y salida funcionan como los de salida.
5. Funciones contra acciones
Una de les preguntas más frecuentes que se plantean a menudo es si delante de un problema es mejor definir una acción o una función.
Función: el criterio más importante para decidir que se debe usar una función es evaluar si esta puede actuar como una función matemática que, dados unos parámetros, puede retornar un valor concreto que se puede utilizar como un miembro de una expresión. Si es así, claramente debemos escribir una función.
Acción: si lo que nos hace falta es actualizar uno de los parámetros o inicializar uno que no lo está, claramente debemos usar una acción. También se utiliza cuando no se retorna ningún valor o cuando se deben devolver más de uno.
Muchas veces las acciones tienen algunos parámetros de salida, pero se podría dar el caso de que no tenga ninguno como, por ejemplo, en el caso de que la acción lea la información del canal estándar y saque también los resultados directamente por el canal estándar.
6. Acciones y funciones predefinidas
Tanto en el lenguaje algorítmico como en los de programación, hay algunas acciones y funciones ya definidas por defecto. Son muy importantes porque facilitan tareas comunes y se utilizan con mucha frecuencia.
De hecho, ya se han visto algunas en las unidades anteriores.
Entre otras tenemos:
- Funciones de conversión de tipo.
- Acciones y funciones de entrada y salida de datos.
Las funciones de conversión de tipo son esas que transforman una variable de un tipo a otro. Incluyen:
[Ejemplo 14_14]
function integerToReal(x: integer):real;
function realToInteger(x: real):integer;
function charToCode(c: char):integer;
function codeToChar(x: integer):char;
int main() {
int x;
float y;
char c;
y = (float) x;
x = (int) y;
x = (int) c;
c = (char) x;
}
Las acciones/funciones de entrada y salida de datos son esas que permiten recibir datos del exterior (teclado, ficheros, etc.) y mostrar datos al exterior. Incluyen:
[Ejemplo 14_15]
function readInteger(): integer;
function readReal(): real;
function readChar(): char;
function readString(): string;
action writeInterger(in x: integer);
action writeReal(in x: real);
action writeChar(in x: char);
action writeString(in x: string);
int main() {
int x;
float y;
char c;
string s;
scanf("%d", &x);
scanf("%f", &y);
scanf("%c", &c);
scanf("%s", s);
printf("%d ", x);
printf("%f ", y);
printf("%c ", c);
printf("%s ", s);
return 0;
}
7. Modularización
Hemos visto cómo los lenguajes de programación permiten definir acciones y funciones, parecidas a subprogramas, que realizan unas tareas concretas y que pueden ser reutilizadas. También hemos visto que algunas de estas acciones y funciones vienen ya predefinidas dentro del lenguaje mientras que la mayoría serán definidas por el usuario.
Para mantener el conjunto de acciones y funciones ordenadas y que se puedan utilizar en diferentes programas de manera fácil, los lenguajes permiten crear librerías.
Estas librerías constan de dos partes:
- Un fichero de texto que incluye las cabeceras de las acciones y funciones que la componen y que en C tienen siempre la extensión .h.
- El código de las acciones y funciones, que también tendrá una extensión .c, pero que solamente tendrá el código de las acciones y funciones, sin tener un main.
Cuando se tengan que utilizar desde algún otro programa solamente se incluirán en el programa el fichero de cabeceras.h. La sintaxis para incluirlas es:
Concretamente, la librería que incluye las cabeceras de las acciones y funciones de entrada y salida de datos se llama en C stdio.h. Cuando queremos utilizarla hay que incluir en el programa:
Hay muchos ejemplos de librerías, por ejemplo, se podrían crear:
- Librerías de funciones matemáticas.
- Librerías de funciones y acciones de tratamiento de fechas.
- Librerías de funciones de tratamiento de cadenas de caracteres.
La posibilidad de crear las librerías facilita la reutilización del código y estandarización de la manera de trabajar.
8. Ejercicios de autoevaluación
1. Diseñad una función que dado un entero n calcule los primeros n números de la serie Fibonacci.
2. Diseñad una acción que, dados un real que representa el saldo de una cuenta corriente y otro real que representa un cargo o imposición, actualice el saldo de la cuenta.
3. Diseñad una función que calcule n (real) elevado a la potencia m (entero).
4. Diseñad una acción que, dados tres números reales que representan los coeficientes de una ecuación de segundo grado, retorne sus raíces, en caso de que existan. En caso contrario, que inicialice las raíces a 0.
Recordad que dada la ecuación A * x2 + B * x + C las raíces se calculan:
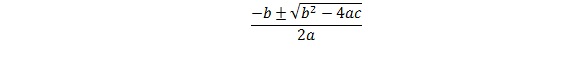
Si la expresión dentro de la raíz es negativa quiere decir que la ecuación no tiene raíces. Podéis suponer que la función raíz cuadrada está ya definida y su cabecera es:
function squareRoor(x: real ): real;
4b. Declarad las variables necesarias para llamar a la acción del ejercicio anterior e indicad cómo se llamaría.
5. Para cada apartado siguiente, decidid si es mejor una acción o una función y definid su cabecera (solamente se pide la cabecera, no hay que diseñar ningún algoritmo).
- Dadas las dimensiones de una pared (altura y anchura) y el precio de pintura por metro cuadrado, determinad el coste total de pintura necesario para pintar la pared.
- Dado el consumo total de agua acumulado desde el mes de enero hasta junio (ambos incluidos), leed por el canal estándar el consumo del resto de meses (desde julio a diciembre, ambos incluidos), y retornadlo acumulado al total del consumo de los 6 primeros meses.
- Dados dos números enteros intercambiad los valores de ambas variables siempre que ambas sean diferentes de cero.
- Dado un entero retornad la suma de sus divisores.
5b) Declarad las variables necesarias para llamar a las acciones del ejercicio anterior e indicad cómo se llamarían.
9. Soluciones
- Diseñad una función que dado un entero n calcule los primeros n números de la serie Fibonacci.
[Ejemplo 14_16]
function fib ( n: integer ): integer;
var
i, value, n+1, n+2: integer;
end var
if n < 3 then
value:= 1;
else
n+1:= 1;
n+2:= 1;
for i:= 3 to n do
value:= n+1 _ n+2;
n+2:= n+1;
n+1:= value;
end for
end if
return value;
end function
int fib( int number) {
int i, value, n+1, n+2 ;
if (n < 3) {
value= 1;
} else {
n+1=1;
n+2=1;
for (i= 3 ; i<=n; i++) {
value= n+1 _ n+2;
n+2= n+1;
n+1= value;
}
}
return value;
}
2. Diseñad una acción que, dados un real que representa el saldo de una cuenta corriente y otro real que representa un cargo o imposición, actualice el saldo de la cuenta.
[Ejemplo 14_17]
action updateBalance(inout balance:real, in amount:real)
balance:= balance + amount;
end action
{només cal actualitzar el saldo (balance) sumant-li la quantitat (amount).}
void updatebalance(float *balance, float amount) {
*balance = *balance _ amount
}
3. Diseñad una función que calcule n (real) elevado a m (entero)
[Ejemplo 14_18]
function toPower(base: real, power: integer): double
var
total: real;
i: integer;
end var
total:=1;
for i:=1 to power do
total:= total*base
end for
return total;
end function
double power(float base, int power) {
float total;
int i;
total = 1;
for (i = 1; i <= power; i++) {
total = total*base;
}
return total;
}
4. Diseñad una acción que, dados tres números reales que representan los coeficientes de una ecuación de segundo grado, retorne sus raíces, en caso de que existan. En caso contrario, que inicialice las raíces a 0.
Recordad que dada la ecuación A * x2 + B * x + C las raíces se calculan:
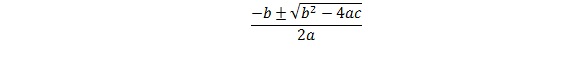
Si la expresión dentro de la raíz es negativa quiere decir que la ecuación no tiene raíces. Podéis suponer que la función raíz cuadrada está ya definida y su cabecera es:
ALGORITMO: function squareRoor(x: real ): real;
C: double squareRoot(double x);
[Ejemplo 14_19]
action roots(in a: float, in b:float, in c:float, out root1:float, out root2:float):
var
temp: real;
end var
temp:= b*b -4.0*a*c;
if temp < 0 then
root1:=0;
root2:=0;
else
root1:= (-b+squareRoot(temp))/2.0*a;
root2:= (-b-squareRoot(temp))/2.0*a;
end if
end action
void roots(float a, float b, float c, float *root1, float *root2) {
float temp;
temp = b*b -4.0*a*c;
if (temp < 0) {
*root1= 0;
*root2= 0;
} else {
root1= (-b+squareRoot(temp))/2.0*a;
root2= (-b-squareRoot(temp))/2.0*a;
}
}
4b. Declarad las variables necesarias para llamar a la acción del ejercicio anterior e indicad cómo se llamaría.
[Ejemplo 14_20]
var
a, b, c: real;
root, root2: real;
end var
{aquí se inicializarían las variables a, b y c}
roots(a, b, c, root1, root2);
int main() {
float a, b, c;
float root1, root2;
/* aquí se inicializarían las variables a, b y c */
roots(a, b, c, &root1, &root2);
}
5. Para cada apartado siguiente, decidid si es mejor una acción o una función y definid su cabecera (solamente se pide la cabecera, no hay que diseñar ningún algoritmo).
5.a.1) Dadas las dimensiones de una pared (altura y anchura) y el precio de pintura por metro cuadrado, determine el coste total de pintura necesario para pintar la pared.
5.a.2) Dado el consumo total de agua acumulado desde el mes de enero hasta junio (ambos incluidos), lea por el canal estándard el consum del resto de meses (desde julio a diciembre, ambos incluidos), y lo retorne acumulado al total del consumo de los 6 primeros meses.
5.a.3) Dados dos números enteros intercambie los valores de ambas variables siempre que ambas sean diferentes de cero.
5.a.4) Dado un entero retorne la suma de sus divisores.
5.a.1) function getCost(height: real, width: real, price_m: real): real
5.a.2) function getTotalConsumption(AcumGenJun: real): real
o
action getTotalConsumption(inout consum: real)
5.a.3) action exchange( inout a: integer, inout b: integer)
5.a.4) function sumDiv (number: integer):integer
float getCost(float height, float width, float price);
/*5.a.2*/
float getTotalComsumption(float acumGenJun);
/*o*/
void getTotalComsumption(float *acumGenJun);
/*5.a.3*/
void exchange(int *a, int *b);
/*5.a.4*/
int sumDiv(int number);
5.b) Declarad las variables necesarias para llamar a las acciones del ejercicio anterior e indicad como se llamarían
5.b.2)
action getTotalConsumption(inout acumGenJun: real)
var
consum: float;
end var
{código de inicialización ... }
getTotalConsumption(consum);
5.b.3)
action exchange( inout a: integer, inout b: integer)
var
a, b: integer;
end var
{código de inicialización ... }
exchange(a, b);
/*5.b.2)*/
void getTotalComsumption(float *acumGenJun);
float consum;
/*código de inicialitzación ... */
getTotalConsumption(&consum);
/*5.b.3)*/
void exchange(int *a, int *b);
int a, b;
/*código de inicialitzación ... */
exchange(&a, &b);
Resumen
En esta unidad hemos visto cómo podemos extender los elementes elementales del lenguaje algorítmico mediante las acciones y funciones.
La importancia de estos elementos nuevos reside en dos aspectos principales:
- Evitar tener que repetir código. Delante de un problema, como hemos visto en el cálculo de los números combinatorios, donde hace falta repetir diversas líneas de código, definimos una función o acción que contenga dichas líneas de código que dan solución al problema concreto y que, mediante el paso de parámetros, podemos ejecutar dicho código para diferentes valores de las variables, tantas veces como queramos.
- Poder diseñar algoritmos complejos de una manera más simple y estructurada. Nos permite descomponer problemas complejos en subproblemas más sencillos e independientes entre sí. Esta técnica se conoce como diseño descendiente. Este aspecto es más importante que el primero, ya que es el que nos permite no solo resolver el problema sino conseguir soluciones con funcionalidades independientes que sean más elegantes, fáciles de entender y de mantener.
Además, los lenguajes de programación ya incluyen conjuntos de acciones y funciones predefinidas, como son las de lectura y escritura de datos y las de conversión de tipos.
También permiten crear librerías con acciones y funciones definidas por los usuarios que se pueden utilizar siempre que se necesiten facilitando la reutilización del código y estandarizando la forma de trabajar.